Naive Bayes is a probabilistic machine learning algorithm based on the Bayes Theorem, used in a wide variety of classification tasks.
In this article, we shall be understanding the Naive Bayes algorithm and its essential concepts so that there is no room for doubts in understanding.
Naive Bayes is a simple but surprisingly powerful probabilistic machine learning algorithm used for predictive modeling and classification tasks.
Some typical applications of Naive Bayes are spam filtering, sentiment prediction, classification of documents, etc. It is a popular algorithm mainly because it can be easily written in code and predictions can be made real quick which in turn increases the scalability of the solution.
The Naive Bayes algorithm is traditionally considered the algorithm of choice for practical-based applications mostly in cases where instantaneous responses are required for user’s requests.
It is based on the works of the Rev. Thomas Bayes and hence the name. Before starting off with Naive Bayes, it is important to learn about Bayesian learning, what is ‘Conditional Probability’ and ‘Bayes Rule’.
Bayesian learning is a supervised learning technique where the goal is to build a model of the distribution of class labels that have a concrete definition of the target attribute. Naïve Bayes is based on applying Bayes’ theorem with the naïve assumption of independence between each and every pair of features.
Let us start with the primitives by understanding Conditional Probability with some examples:
Example-I
Consider you have a coin and fair dice. When you flip a coin, there is an equal chance of getting either a head or a tail. So you can say that the probability of getting heads or the probability of getting tails is 50%.
Now if you roll the fair dice, the probability of getting 1 out of the 6 numbers would be 1/6 = 0.166. The probability will also be the same for other numbers on the dice.
Example-II
Consider another example of playing cards. You are asked to pick a card from the deck. Can you guess the probability of getting a king given the card is a heart?
The given condition here is that the card is a heart, so the denominator has to be 13 (there are 13 hearts in a deck of cards) and not 52. Since there is only one king in hearts, so the probability that the card is a king given it is a heart is 1/13 = 0.077.
So when you say the conditional probability of A given B, it refers to the probability of the occurrence of A given that B has already occurred. This is a typical example of conditional probability.
Mathematically, the conditional probability of A given B can be defined as:
P(A and B) / P(B)
Bayes’ Theorem helps you examine the probability of an event based on the prior knowledge of any event that has a correspondence to the former event. Its uses are mainly found in probability theory and statistics.
Consider for example the probability that the price of a house is high can be calculated better if we have some prior information like the facilities around it compared to another assessment made without the knowledge of the location of the house.
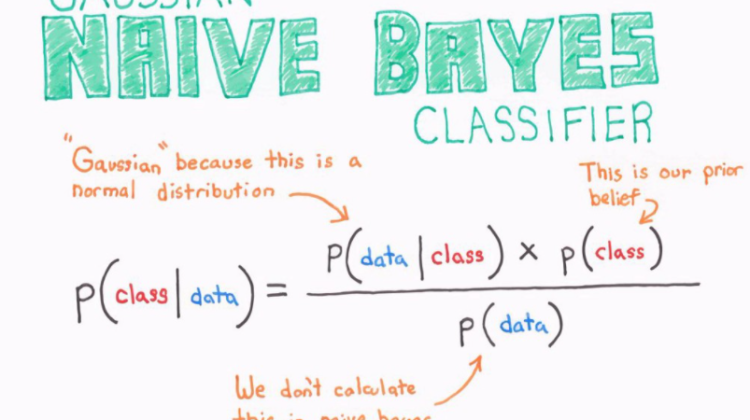
P(A|B) = [P(B|A)P(A)]/[P(B)]
The equation above shows the basic representation of the Bayes’ theorem where A and B are two events and:
P(A|B): The conditional probability that event A occurs, given that B has occurred. This is termed as the posterior probability.
P(A) and P(B): The probability of A and B without any correspondence with each other.
P(B|A): The conditional probability of the occurrence of event B, given that A has occurred.
The Bayes’ Theorem can be reformulated in correspondence with the machine learning algorithm as:
posterior = (prior x likelihood) / (evidence)
Consider a situation where the number of attributes is n and the response is a Boolean value. i.e. Either True or False. The attributes are categorical (2 categories in this case). You need to train the classifier for all the values in the instance and the response space.
This example is practically not possible in most machine learning algorithms since you need to compute 2∗(2^n-1) parameters for learning this model. This means for 30 boolean attributes, you will need to learn more than 3 billion parameters which is unrealistic.
Naive Bayes classifiers in machine learning are a family of simple probabilistic machine learning models that are based on Bayes’ Theorem. In simple words, it is a classification technique with an assumption of independence among predictors.
The Naive Bayes classifier reduces the complexity of the Bayesian classifier by making an assumption of conditional dependence over the training dataset.
Consider you are given variables X, Y, and Z. X will be conditionally independent of Y given Z if and only if the probability distribution of X is independent of the value of Y given Z. This is the assumption of conditional dependence.
In other words, you can also say that X and Y are conditionally independent given Z if and only if, the knowledge of the occurrence of X provides no information on the likelihood of the occurrence of Y and vice versa, given that Z occurs. This assumption is the reason behind the term naive in Naive Bayes.
The likelihood can be written considering n different attributes as:
n
P(X₁...Xₙ|Y) = π P(Xᵢ|Y)
i=1
In the mathematical expression:
X represents the attributes & Y represents the response variable.
So, P(X|Y) becomes equal to the product of the probability distribution of each attribute given Y.
Maximizing a Posteriori
If you want to find the posterior probability of P(Y|X) for multiple values of Y, you need to calculate the expression for all the different values of Y.
Let us assume a new instance variable X_NEW. You need to calculate the probability that Y will take any value given the observed attributes of X_NEW and given the distributions P(Y) and P(X|Y) which are estimated from the training dataset.
In order to predict the response variable depending on the different values obtained for P(Y|X), you need to consider a probable value or the maximum of the values.
Hence, this method is known as maximizing a posteriori.
Maximizing Likelihood
You can simplify the Naive Bayes algorithm if you assume that the response variable is uniformly distributed which means that it is equally likely to get any response.
The advantage of this assumption is that the priori or the P(Y) becomes a constant value.
Since the a priori and the evidence become independent from the response variable, they can be removed from the equation.
So, maximizing the posteriori becomes maximizing the likelihood problem.
Consider a situation where you have 1000 fruits which are either ‘banana’ or ‘apple’ or ‘other’. These will be the possible classes of the variable Y.
The data for the following X variables all of which are in binary (0 and 1):
The training dataset will look like this:
Now let us sum up the training dataset to form a count table as below:
The main agenda of the classifier is to predict if a given fruit is a ‘Banana’ or an ‘Apple’ or ‘Other’ when the three attributes (long, sweet and yellow) are known.
Consider a case where you’re given that a fruit is long, sweet and yellow and you need to predict what type of fruit it is.
This case is similar to the case where you need to predict Y only when the X attributes in the training dataset are known. You can easily solve this problem by using Naive Bayes.
The thing you need to do is to compute the 3 probabilities, i.e. the probability of being a banana or an apple or other. The one with the highest probability will be your answer.
Step 1
First of all, you need to compute the proportion of each fruit class out of all the fruits from the population which is the prior probability of each fruit class.
The Prior probability can be calculated from the training dataset:
The training dataset contains 1000 records. Out of which, you have 500 bananas, 300 apples and 200 others. So the priors are 0.5, 0.3 and 0.2 respectively.
Step 2
Secondly, you need to calculate the probability of evidence that goes into the denominator. It is simply the product of P of X’s for all X:
Step 3:
The third step is to compute the probability of likelihood of evidence which is nothing but the product of conditional probabilities of the 3 attributes.
The Probability of Likelihood for Banana:
Therefore, the overall probability of likelihood for banana will be the product of the above three,i.e. 0.8 * 0.7 * 0.9 = 0.504.
Step 4:
The last step is to substitute all the 3 equations into the mathematical expression of Naive Bayes to get the probability.
In a similar way, you can also compute the probabilities for ‘Apple’ and ‘Other’. The denominator is the same for all cases.
Banana gets the highest probability, so that will be considered as the predicted class.
Types of Naive Bayes Classifiers
The main types of Naive Bayes classifier are mentioned below:
- Multinomial Naive Bayes — These types of classifiers are usually used for the problems of document classification. It checks whether the document belongs to a particular category like sports or technology or political etc and then classifies them accordingly.
The predictors used for classification in this technique are the frequency of words present in the document.
- Complement Naive Bayes — This is basically an adaptation of the multinomial Naive Bayes that is particularly suited for imbalanced datasets.
- Bernoulli Naive Bayes — This classifier is also analogous to multinomial Naive Bayes but instead of words, the predictors are Boolean values. The parameters used to predict the class variable accepts only yes or no values,
For example, if a word occurs in the text or not.
- Out-of-Core Naive Bayes — This classifier is used to handle cases of large scale classification problems for which the complete training dataset might not fit in the memory.
- Gaussian Naive Bayes — In a Gaussian Naive Bayes, the predictors take a continuous value assuming that it has been sampled from a Gaussian Distribution. It is also called a Normal Distribution.
For more on Probability Distributions — Mathematics for Machine Learning Part-5
The Naive Bayes algorithm has both its pros and its cons:
Pros
- It is easy and fast to predict the class of the training data set.
- It performs well in multiclass prediction.
- It performs better as compared to other models like logistic regression while assuming the independent variables.
- It requires less training data.
- It performs better in the case of categorical input variables as compared to numerical variables.
Cons
- The model is not able to make a prediction in situations where the categorical variable has a category that was not observed in the training data set and assigns a 0 (zero) probability to it.
This is known as the ‘Zero Frequency’. You can solve this using the Laplace estimation.
- Since Naive Bayes is considered to be a bad estimator, the probability outputs are not taken seriously.
- Naive Bayes works on the principle of assumption of independent predictors, but it is practically impossible to get a set of predictors that are completely independent.
Laplace Correction
When you have a model with a lot of attributes, it is possible that the entire probability might become zero because one of the feature’s values is zero.
To overcome this situation, you can increase the count of the variable with zero to a small value like in the numerator so that the overall probability doesn’t come as zero.
This type of correction is called the Laplace Correction. Usually, all naive Bayes models use this implementation as a parameter.
Applications
There are a lot of real-life applications of the Naive Bayes classifier, some of which are mentioned below:
- Real-time prediction — It is a fast and eager machine learning classifier, so it is used for making predictions in real-time.
- Multi-class prediction — It can predict the probability of multiple classes of the target variable.
- Text Classification/Spam Filtering/Sentiment Analysis — They are mostly used in text classification problems because of its multi-class problems and the independence rule. They are also used for identifying spam emails and also to identify negative and positive customer sentiments on social platforms.
- Recommendation Systems — A Recommendation system is built by combining Naive Bayes classifier and Collaborating Filtering. It filters unseen information and predicts whether the user would like a given resource or not using machine learning and data mining techniques.
Improving Model
You can improve the power of a Naive Bayes model by following these tips:
- Transform variables using transformations like BoxCox and YeoJohnson to make continuous features to normal distribution.
- Use Laplace Correction for handling zero values in X variables and to predict the class of test data set for zero frequency issues.
- Check for correlated features and remove the highly correlated ones because they are voted twice in the model and might lead to over inflation.
- Combine different features to make a new product which makes some intuitive sense.
- Provide more realistic prior probabilities to the algorithm based on knowledge from business. Use ensemble methods like bagging and boosting to reduce the variance.
Hope you enjoyed and made the most out of this article! Stay tuned for my upcoming blogs! Make sure to CLAP and FOLLOW if you find my content helpful/informative!
To contact, or for further queries, feel free to drop a mail at — tp6145@bennett.edu.in
