A Step by Step Guide
If you always wanted to learn decision trees, just by reading this, you’ve received a beautiful opportunity, a stroke of luck, I might say. But as entrepreneurs say, “it’s not enough to be in the right place; you also need to take the opportunity when it comes”. So, consider giving yourself some time and get comfortable, because what’s coming it’s not the shortest guide, but it might be the best.
Decision trees are the foundation of the most well performing algorithms on Kaggle competitions and real-life. An indicator of this is that you are certainly going to collide with a “max_depth” on almost every ensemble. That’s precisely the reason why the story you are about to read uses the most relevant hyperparameters to build its narrative.
I never really learn decision trees until I decided to start looking at every hyperparameter. After studying them in detail, all the fog in my mind slowly vanished. I wrote this thinking of the guide I wish I had when I started looking for information, so it’s intended to be very easy to follow.
Don’t get me wrong. I don’t want to look like a smug repeating the typical smarty phrase “you should know all the foundations before doing anything” because I don’t believe in it that much.
The learning process is not linear, and if you want to train your first model, maybe it’s better for you just to know what a random forest is and go for it. It’s a significant step!. But after your first model training, I’m sure that you will realize that some problems may arise.
You will have neither the compute infrastructure nor the time to try every hyperparameter combination. Understanding what’s happening behind the scenes when you tweak them will give you a smarter starting point.
I can assure you, and remember this one, the next time you define your hyperparameter range, you will start hypothesizing on the best combination, checking which one worked the best. That exercise will improve your skills a lot more than just a blindfolded grid-search.
For this guide, you don’t need any prior knowledge of decision trees. That’s the magic. The algorithm will be built upon the hyperparameters. We can kill two birds with one shot: learn how decision trees work and how the hyperparameters modify their behavior. I really encourage you to read every hyperparameter because we will be building blocks on the algorithm’s underlying mechanics while we review them.
Just for the sake of the conversation, I want to clarify the parameters used on the scikit-learn implementation for classification. The idea is to mix intuition and math to create the perfect learning combination for you.
Note: At the time this is being written, there are 12 parameters not deprecated on the scikit-learn documentation. As there are so many, we will focus just on 6. But if you support this, I will certainly come back with the others. Also, the word hyperparameter and parameter will be used interchangeably.
Decision trees are implemented on scikit using an optimized version of the CART algorithm. The procedure is to ask questions about the data to split it into two groups. This is very important because other implementations can split the data into more than two groups at once.
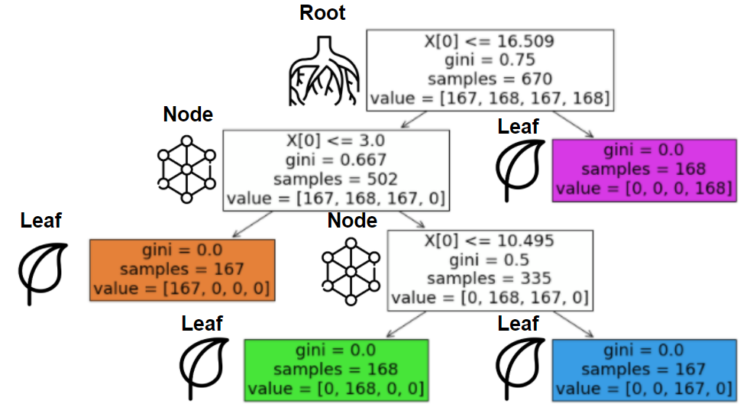
This happens over and over until one of our beloved parameters stops this process or when the data cannot be split anymore (1 sample). Before the first question, the place where we have all the data is called the “root”. After that, every subset of samples is a “node” if there is a split after it. If this node can’t be split, we will call it a “leaf”.
On the image, you can see the overall structure. The illustration and title are on the left of its corresponding boxes. If you don’t understand what’s happening here, don’t hesitate to keep reading, everything will be clear after some minutes.
Ok, that’s a pretty general approximation, but you might have some fair questions like: “how to decide the variable for the split?”, “how to choose the threshold for the split?”, “can I use the same feature again?” or “is it the depth related to the number of splits?”, among many others.
The goal of what you are going to read is to answer those questions and a lot more. On every (hyper)parameter, you will discover new clues that will help you to actually see how trees grow. And, if someday someone gives you some data, a pencil, and a piece of paper, you will be well equipped to solve the problem by yourself (super useful!).
Are you ready? Let’s do it!
This parameter isn’t a “game-changer” but it’s pretty useful to dispel how the basic mechanics of decision trees work. As the old saying says, “let’s start by the beginning”.
As we saw, on every iteration, we have to determine which feature we will select to ask the question to our data. Because of that, we should have a method to rank different options.
The functions to measure the quality of the split that we will review are two: Gini and entropy.
Gini: a great way to understand it is by checking Wikipedia’s definition “Gini impurity is a measure of how often a randomly chosen element from the set would be incorrectly labeled if it was randomly labeled according to the distribution of labels in the subset”.
To better explain this concept, we will use the most original example that I could think of: balls. Imagine a case where we have 5 balls, we know the weight of these balls, they can be big or small and red or green.
The goal is to predict the color of the balls based on their weight and size. Now is when we should start using our Gini measurement to choose if we will split our data based on the ball’s weight or size.
Before the mathematical formulation, let’s try to figure out what this measurement is trying to do. Let’s replicate the Gini impurity definition for this particular case in our “root node”. First, we need to randomly select an element, and after that, we need to label it following the original distribution.
In this case, we selected the big green ball of 4 kilos, and we should label it as red with a probability of 0.6 and as green in the remaining 0.4. The problem is that we can’t calculate it with just one example. The Gini impurity aims to determine how often, after this procedure, we would end up with an incorrectly labeled sample as a whole.
A possible solution could be to simulate this process and repeating it enough times to get a good estimate. We can try that with the following code.
You will probably get something like that number. That’s the probability of mislabeling a sample, and we’ve used none other information than the distribution of the target value.
The calculation is needed for every iteration, and doing it in that way can be a bit slow, but don’t be scared. We can do better than that. If we go back to our flowchart, we can use probabilities to create a deterministic formula.
As you can see the probability of getting it wrong is the sum of the probability of choosing a green sample labeled as red plus the opposite case.
Awesome, we just calculate our first Gini impurity! Now we can make an extra effort to generalize what we just did for n classes. The first step is to select the probability of choosing the first class (P(Class1)), and then multiply it by the probability of mislabeling it, which is (1-P(Class1)). As we saw in our most recent case, we have to sum this calculation for every class.
Unbelievable! Now we can say that we really understand how we calculate the Gini impurity. After seeing all of this information, we can assert that this is an attempt to measure how mislabeled our node will be. The algorithm will select the variable which minimizes it.
Ok, we are getting closer to taking our first decision, but nobody said it would be easy. We still have to solve some other minor issues. First, how we deal with different variable types?.
Well, categorical variables must be “one-hot-encoded” which means transforming categories into binary variables. Therefore the split is pretty intuitive. For continuous variables is a little different: the selection of the threshold should be optimized to create the best possible split.
To show you the importance of selecting the exact number of the split for a continuous feature, I will show you two possibles splits based on the weight. You will see a significant difference between choosing a “good” or a “bad” split using the same variable!. We can start using 3.5 kilos to split the balls and calculate the Gini.
Ok, we have learned how to calculate one particular split, but what to do when we have a split with two nodes (which will always be the case when we want to deliberate between splits). As you saw in the figure, we have to weight them based on the samples belonging to each node. Now let’s try with 2.5 kilos as our split criteria.
It looks better, and it’s objectively better. The algorithm chooses the best Gini impurity to do this split, and now we know how to compare them. In case you are still a little skeptical about all the beautiful balls we just saw, we can invoke scikit-learn for you to believe me.
The visualization is showing the variable used; “X[0]” which is the weight for this case. It also shows the Gini values for every node, the number of samples, and equals to “value” you can see the distribution of the classes (green at the left and red at the right). Everything was exactly as we expected it to be.
I just earn some credibility, don’t I?. To take advantage of this ephemeral moment of trust, I will show you an interesting last thing before we move on. As you know, we have another feature: the size. That’s a binary variable, and because of that, it’s easy to determine the threshold to be selected (any value between 0 and 1).
Wow! The size is as good as the weight. So, why did scikit chose the latter?. Don’t worry. The implementation doesn’t have any preferences. If there is a tie, it will make a random choice, and that’s why the “random_state” becomes relevant. This parameter controls the randomness of decisions like these ones. Changing the parameter from 42 to 40 will do the trick.
“X[1]” represents the weight, and the threshold was obviously set to 0.5. We learned that the same tree can take a different path if we don’t clarify the “random_state”. There can be ties among variables!.
After the last magical trick, we can close the Gini criteria discussion to give way to our next guest: entropy
Entropy: If the Gini impurity tries to measure how mislabeled the node will be, the entropy will try to estimate how uncertain the outcome is.
The history behind entropy is fantastic, starts with thermodynamics, advances to information theory to reach us here, on decision trees. It’s incredible enough to deserve its own blog post (in which I’m working). So, to avoid straying so far off the road, I will straight away drop the formula. I know it might come out of nowhere, but it’s the price for a goal-oriented post.
For our initial level, we know that the probabilities are 0.6 and 0.4 for red and green balls, respectively. We can calculate the entropy for that case.
You can try on your own combinations like [1,0] or [0.5,0.5]. With the first, the entropy is 0, zero uncertainty, for the latter is 1. You can see that our 0.97 is very close to the full uncertainty scenario.
If we change the criterion parameter to “entropy”, scikit will display it on the visualizations.
Just to summarize, we can compare how Gini and entropy will fluctuate given every possible combination for 5 balls. Below a little gift for you, the calculation “from scratch” of our two different possible parameters.
In the last section, we assumed that the algorithm would look for the best split every time we have a continuous variable. But “splitter” gives us some flexibility on this assumption. There are two options: “best” and “random”. The default parameter is “best”.
When choosing “best”, unsurprisingly, the algorithm will choose the best split — like in the last section — , but when choosing “random”, the split will be just a random number. To show this clearly, I will present the same example we used before, but this time using only the weight as the explanatory variable.
As you can see, the threshold was set to 3.975, giving us an unfortunate split. It’s important to say that this “poorly” split is not always a bad thing. Now you know that the algorithm looks by default the best split on every iteration, but that’s not necessarily the optimal way to find the global optimum. Using a random split could lead to some variability, which sometimes helps us find a better tree.
To understand how “max_depth” works, we have to look at the tree’s internal structure. Do you remember that we never let the tree grow more than one split? That was because we force the algorithm to stay on a max depth of 1. The depth is not the number of splits. It’s the maximum number of generations after the root node.
If you think that a node receiving an arrow from another is a daughter, setting the max depth to one will allow the root node to be, at tops, a mother. If we set the parameter to two, the root node can’t go further than a grandmother, and that logic goes on and on.
For this and the following sections, we will use a new example, I know that you will miss the balls, but the new one will do a better job to explain what’s coming (and it’s about balls too). Imagine a simple classification case where you only have one feature (weight in ounces) and four classes (types of balls). To make this even easier, let’s assume a direct relation between them: when the variable is within a specific range, it will always belong to the same class (as the last image).
As the code snippet shows, if our feature is between 0 and 3, the class will always be a golf ball, the same behavior is expected for the other cases. So let’s understand how “max_depth” impacts the model. Let’s train the first one using a “max_depth” of 1.
The model defined the optimal threshold (10.495). The classes on the left side belonged to our 0 or 1, and those on the right to 2 and 3. The model hadn’t the chance to create another step to really separate them. So let’s try a “max_depth” of 2 and see what is happening.
The first important thing for you to notice is that variables can be repeated, so using a “max_depth” of the same size of the number of features does not necessarily cover every base. If a variable is the best split in a particular scenario, it can show up independent of its first appearances.
Using a “max_depth” of 2 it’s actually enough in this case to separate perfectly every branch. But there is no rule of thumb to determine how profound the tree should go. Let’s go for the exact same case, but changing the test split from 0.2 to 0.33.
In this case, setting a “max_depth” of 2 wasn’t enough to separate every case. This was due to the first split, which happened in a bigger threshold. Using a “max_depth” of 3 will do the trick in this case.
Here comes the second important thing to learn, subtle changes in the structure of the data may result in different depths of the decision tree, even with just one variable. This is something critical because forces us to cover wider ranges if the variables have a lot of information like in this case.
It’s impossible to close this section without covering underfitting and overfitting. Underfitting is when the tree is not complex enough to capture the real relationship between the variables. For instance, when we set “max_depth” to 1, the model didn’t learn how to differentiate between baseball and golf balls.
Overfitting is when the model becomes so complex that it starts capturing noise instead of understanding the data’s real underlying structure. Our data didn’t have any noise. Because of that, overfitting wasn’t possible. In general, there is a lot of noise in the data, so letting “max_depth” to fly so freely might lead to overfitting.
Min impurity decrease is a way to control if a split it’s really worth it. There are times that, if we keep splitting our nodes, it will do more harm than good. If we don’t use this parameter, the model could tend to overfit the data.
Imagine that, when we were weighing the balls, by mistake, three baseball balls were weighted instead of one. The data was stored with a value of 21.1, and the class was set to 1. Let’s go back to our example, without any restriction on “min_impurity_decrease”.
The model now thinks that every weight higher than 21.024, it’s a baseball ball. If you think about it, it’s certainly a mistake, maybe a new basketball ball is a little higher than 21 ounces, but the model will mistakenly predict it as a baseball ball.
But “min_impurity_decrease” can save the day. As you can see, every node has its own Gini value. This parameter allows us to choose if the split it’s worth it or it doesn’t. For the last example, the Gini value of the problematic node was 0.01, which appears to be very low to do a split. If we set this parameter to 0.01 or higher, we limit the split, solving our overfitting problem.
With the new changes, the model accepts a little impurity on the node, but we know that the reward is that it can effectively ignore the random noise that was added to the data. Our new tree is able to pass the test that the previous one couldn’t.
The trade-off between underfitting and overfitting might look like a déjà vu, but setting a value that it’s not so high and not extremely low, is the same balance that we wanted to achieve with the “max_depth”, and it will be the same on our last hyperparameter: “min_samples_split”.
“Min_samples_split” depends a lot more on the number of the initial samples than the last one. This parameter can be set to an integer, and if that is the case, the tree will decide to move forward with the split if the parameter is lower than the number of samples of the node. Otherwise, the node will become a leaf.
If a fraction is given, it will multiply the fraction per the total number of samples at the root, and that will be the number to be set for the algorithm. For our very last example, we could see that the last useful node was split with 399 samples. Using any value between 202 and 399 will be enough to prevent overfitting, and obtained the same tree as before.
We learned quite a lot today, but it’s always a great idea to see what we’ve accomplished. The highlights today were:
- We saw the structure of decision trees, and we now know what a “root” a “node” and a “leaf” are.
- We learned that the “criterion” hyperparameter defines if a split is “good” or “bad”.
- We understood that randomness is part of the process. We saw how “splitter” could add some variability to the model, while “random_state” could give us reproducible conditions.
- We dealt with underfitting and overfitting using “max_depth”, “min_impurity_decrease”, and “in_samples_split”.
Good enough for a single post, don’t you think?.
I really hope that this blog was somehow interesting to you. Tell me in the comments if you liked it!
[1] Scikit-learn decision trees documentation.
[2] Stackoverflow post.
