Due to digitization, a huge volume of data is being generated across several sectors. Access to big data helps us to better understand the business and build better models.
On the other hand, not all features in the datasets are equally important for training the machine learning models.
Some of them might be even irrelevant and thus provide a bias in the outcome. That’s why the common approach is to reduce the dimensionality of the dataset.
Dimensionality reduction in data mining focuses on representing data with a minimum number of dimensions such that its properties are not lost and hence reducing the underlying complexity in processing the data.
The two most commonly used dimensionality reduction techniques include s linear discriminant analysis (LDA) and, principal component analysis (PCA).
In this article, we will focus on PCA. Specifically, I will demonstrate how to use PCA for dimensionality reduction in Python.
Apart from that, I will give you an introduction to the methodology of PCA and, describe how it works. Finally, I will also explain what is the difference between LDA and PCA.
What is this Principal Component Analysis (PCA)?
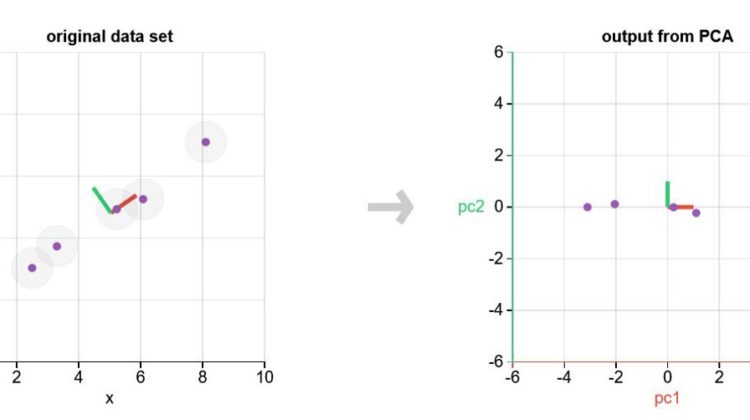
Principal Component Analysis is a feature extraction technique that generates new features which are a linear combination of the initial features. PCA maps each instance of the given dataset present in a d dimensional space to a k dimensional subspace such that k < d.
The set of k new dimensions generated is called the Principal Components (PC). Each of these Principal Components has a linear combination with the original set of a variable.
Let’s think about a dataset with n number of features: x1,x2,x3 ,x4…xn . Then the Principal Component (PC) can be represented as the following.
PC = a1x1 + a2x2 + a3x3 + a4x4 + … + anxn
a1,a2,a3 ,…an values are called principal component loading vectors.
In simple words, PCA is a technique that converts a high dimensional feature space to a set of a small number of features while reducing the data loss as much as possible.
How does principal component analysis work?
Assume that a dataset x(1),x(2),…..xm with n- dimension features. Our goal is to reduce the dimensionality, i.e. we want to reduce the n-dimension data to k-dimension using PCA. Then, the PCA can be described as follow:
- Standardization of the raw data: The raw data should have unit variance and zero mean.
- Compute the covariance matrix of the raw data.
- Compute the eigenvector and eigenvalue of the covariance matrix.
- Sort eigenvalues in descending order and choose the k eigenvectors that correspond to the k largest eigenvalues, where (k < n)
- Construct the projection matrix W from the selected k eigenvectors.
- Transform the original dataset via W to obtain a k-dimensional (reduced) feature subspace.
What is the difference between PCA and LDA?
As I mentioned, both PCA and LDA are linear transformation techniques that are the most commonly used for dimensionality reduction. However, there is one important difference between them.
The principal component analysis ignores class labels altogether and aims to find the principal components to maximize variance in a given set of data. Thus, PCA can be considered as an unsupervised algorithm.
On the other hand, Linear Discriminant Analysis can be considered as a supervised algorithm. LDA computes the linear discriminants that represent the axes to maximize the separation between multiple classes.
Dimensionality Reduction With PCA In Python
To demonstrate how to implement PCA in Python I will use the scikit-learn Python machine learning library and the PCA class.
For this tutorial, I will use Wine Dataset. This dataset is public available here: UCI Machine Learning Repository.
UCI Notes About the Dataset:
- The classes are ordered and not balanced (e.g. there is much more normal wines than excellent or poor ones).
- Outlier detection algorithms could be used to detect the few excellent or poor wines.
- Also, we are not sure if all input variables are relevant. So it could be interesting to test feature selection methods.
Note: for simplicity, we are not going to deep dive into data preprocessing
Let’s first import libraries and read the dataset. Then, we will define the dependent and independent variables.
Next, we split data to train and test sets. To do that we will use the ‘train_test_split’ method from sklearn library. Our split is 80% train and 20% test.
Before we apply PCA we need to scale out data. We will use the StandardScaler method.
Let’s apply PCA
Now, we will train a simple Logistic Regression model.
Let’s make a confusion matrix to evaluate the model.
As we can see, accuracy is 97,2% which is pretty high.
We can also visualize train and test data.
Conclusion
Dimensionality reduction can help us to remove irrelevant or redundant features that may bias our model. One of the most popular methods for dimensionality reduction is PCA.
In this article, I demonstrated how to use PCA for dimensionality reduction in Python. Specifically, I described:
- What is the principal component analysis and how it works,
- what is the difference between LDA and PCA
- how to implement PCA with Python.
