Statistical hypothesis testing allows us to make decisions in the presence of incomplete data. By definition, these decisions are uncertain. Statisticians have developed rigorous methods to evaluate this risk. Nevertheless, some subjectivity is always involved in the decision-making process. The theory is just a tool that helps us make decisions in an uncertain world.
Here, we introduce the most basic ideas behind statistical hypothesis testing. We will follow an extremely simple example: coin tossing. More precisely, we will show how to perform a z-test, and we will briefly explain the mathematical ideas underlying it. This kind of method (also called the frequentist method), although widely used in science, is subject to many criticisms. We will show later a more modern approach based on Bayesian theory. It is very helpful to understand both approaches because many studies and publications still follow frequentist methods.
You need to have a basic knowledge of probability theory for this (random variables, distributions, expectancy, variance, central limit theorem, and so on).
Many frequentist methods for hypothesis testing roughly involve the following steps:
- Writing down the hypotheses, notably the null hypothesis, which is the opposite of the hypothesis we want to prove (with a certain degree of confidence).
- Computing a test statistic, a mathematical formula depending on the test type, the model, the hypotheses, and the data.
- Using the computed value to accept the hypothesis, reject it, or fail to conclude.
Here, we flip a coin n times and we observe h heads. We want to know whether the coin is fair (null hypothesis). This example is extremely simple yet quite useful for pedagogical purposes. Besides, it is the basis of many more complex methods.
We denote the Bernoulli distribution by B(q) with the unknown parameter q.
A Bernoulli variable is:
- 0 (tail) with probability 1-q
- 1 (head) with probability q
Here are the steps required to conduct a simple statistical z-test:
- Let’s suppose that after n=100 flips, we get h=61 heads. We choose a significance level of 0.05: is the coin fair or not? Our null hypothesis is: the coin is fair (q = 1/2):
import numpy as np
import scipy.stats as st
import scipy.special as spn = 100 # number of coin flips
h = 61 # number of heads
q = .5 # null-hypothesis of fair coin
2. Let’s compute the z-score, which is defined by the following formula ( xbar is the estimated average of the distribution). We will explain this formula in the next section, How it works….
xbar = float(h) / n
z = (xbar - q) * np.sqrt(n / (q * (1 - q)))
# We don't want to display more than 4 decimals.
zOut[3]: 2.1999999999999997
3. This p-value is less than 0.05, so we reject the null hypothesis and conclude that the coin is probably not fair.
pval = 2 * (1 - st.norm.cdf(z))
pvalOut[4]: 0.02780689502699718
The coin-tossing experiment is modelled as a sequence of n independent random variables x i ∈ { 0,1 } following the Bernoulli distribution B(q). Each xi represents one coin flip. After our experiment, we get actual values (samples) for these variables. A different notation is sometimes used to distinguish between the random variables (probabilistic objects) and the actual values (samples).
The following formula gives the sample mean (proportion of heads here):
Knowing the expectancy μ = q and variance σ 2 = q ( 1 − q ) of the distribution B(q),we compute:
The z-test is the normalized version of x (we remove its mean, and divide by the standard deviation, thus we get a variable with mean 0 and standard deviation 1):
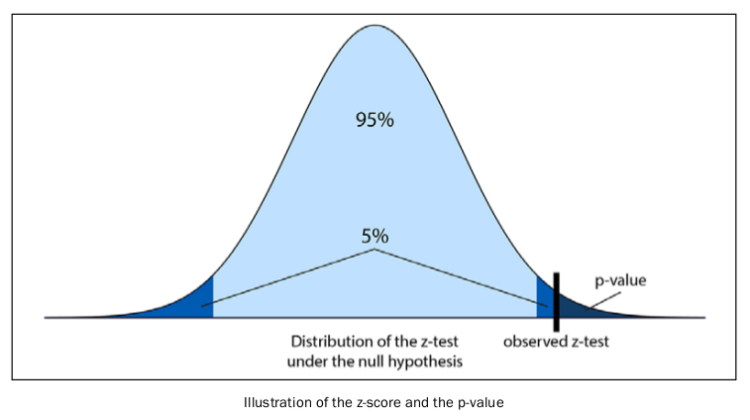
Under the null hypothesis, what is the probability of obtaining a z-test higher than some quantity z 0 ? This probability is called the (two-sided) p-value. According to the central limit theorem, the z-test approximately follows a standard Gaussian distribution N(0,1) for large n, so we get:
The following diagram illustrates the z-score and the p-value:
In this formula, Φ is the cumulative distribution function of a standard normal distribution. In SciPy, we can get it with scipy.stats.norm.cdf . So, given the z-test computed from the data, we compute the p-value: the probability of observing a z-test more extreme than the observed test, under the null hypothesis.
If the p-value is less than five percent (a frequently-chosen significance level, for arbitrary and historical reasons), we conclude that either:
- The null hypothesis is false, thus we conclude that the coin is unfair.
- The null hypothesis is true, and it’s just bad luck if we obtained these values.
We cannot make a conclusion.
We cannot disambiguate between these two options in this framework, but typically the first option is chosen. We hit the limits of frequentist statistics, although there are ways to mitigate this problem (for example, by conducting several independent studies and looking at all of their conclusions).
