
Regularization With Ridge
Both problems related to bias and overfitting can be elegantly solved using Ridge and Lasso Regression. The equation for the line of best fit is still the same for the new two regressions:
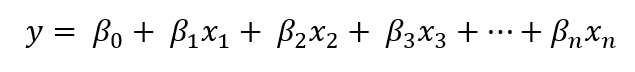
What is changed is the cost function. Both Ridge and Lasso Regression introduce a new hyperparameter to the OLS — 𝜆. Let’s first look at the cost function of Ridge:
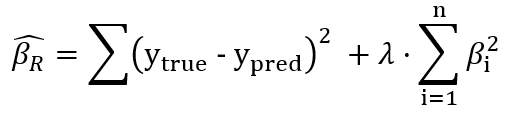
Apart from OLS (the first part), ridge regression squares every individual slope of the feature variables and scales them by some number 𝜆. This is called the Ridge Regression penalty. What this penalty essentially does is shrink all coefficients (slopes). This shrinkage has a double effect:
- We avoid overfitting with lower coefficients. As lambda is just some constant, it has the same scaling effect on all coefficients. For example, by choosing a low value for lambda like 0.1, we get to scale all coefficients both large and small.
- This scaling also introduces some bias to the completely unbiased LR. Think about it this way — if you square a large number, you get an even larger number. By choosing a low value like 0.01 you get to shrink the number a lot. But if you square small numbers such as numbers lower than 1, instead of getting a larger number, you get an even smaller number. And multiplying it by 0.01, you manage to make it even smaller. This way, ridge regression gets to make important features more pronounced and shrink unimportant ones close to 0 which leads to a more simplified model.
You might be saying that the added sum of scaled, squared slopes will be bigger which does not fit the training data as well as the plain-old OLS. It is true but starting with a slightly worse fit, Ridge and Lasso provide better and more consistent predictions in the long run. By introducing a small amount of bias, we get a significant drop in variance.
Let’s see Ridge in action using Scikit-learn. Ridge follows the same API as any other model offered by sklearn. We will work on the Ames Housing Dataset from Kaggle. Using a subset of features, we will predict house prices using Ridge in this section and Lasso in the next one. To make things short, I am loading an already-processed dataset (feature selected, scaled, and imputed):
First, we will fit a LinearRegression model and compare its performance to Ridge using MAE (Mean Absolute Error). Before we do this, there are a few preprocessing required like feature scaling the variables and filling in missing values. So, I will create a simple Pipeline instance to deal with them:
If you want to know more about
pipelinesusingsklearncheck out this article or notebook on Kaggle.
Now, let’s first fit a Linear Regressor:
As you can see, the testing score is significantly lower than training’s which suggests overfitting. Now, let’s try Ridge:
We get almost identical results for Ridge because we chose too small a value for alpha. If you go back to the cost function of Ridge, you can see that if we set lambda to 0, we get plain-old OLS back:
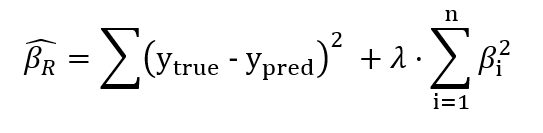
Note that in
sklearnAPI, the hyperparaterlambdais given asalpha. Don’t get confused.
Now, instead of blindly trying out a bunch of values for alpha, we can use cross-validation using RidgeCV. Instead of taking a single value for alpha, RidgeCV takes a list of possible alphas and tries them out using cross-validation, just like GridSearch:
We are passing alphas in the range of 1 and 100 with a step of 5 under a 10-fold cross-validation. After the fit is done, we can get the best alpha using .alpha_ attribute:
>>> ridge.alpha_86
Let’s finally evaluate a Ridge with that hyperparameter and compare it with Linear Regression:
Unfortunately, even with the best value for alpha, we get almost identical results to Linear Regression. (I realized this was a bad dataset for showing Ridge and Lasso much later while writing the article😶).
