Exploring the metric functions used in K Nearest Neighbor (KNN) model
Introduction
If you’re familiar with some of the basic machine learning algorithms that are used in the field, then you’ve probably heard of the k-nearest neighbors algorithm, or KNN. It is the algorithm companies like Netflix or Spotify use in order to recommend different movies to watch or songs to listen to.
The concept of finding nearest neighbors may be defined as “the process of finding the closest point to the input point from the given data set”. The algorithm stores all the available cases (test data) and classifies new cases by majority votes of its k neighbors. When implementing KNN, the first step is to transform data points into their mathematical values (vectors). The algorithm works by finding the distance between the mathematical values of these points. It computes the distance between each data point and the test data and then finds the probability of the points being similar to the test data. Classification is based on which points share the highest probabilities. The distance function can be Euclidean, Minkowski or the Hamming distance.
Euclidean Distance Function
Euclidean distance can simply be defined as the shortest between the 2 points irrespective of the dimensions. The most common way to find the distance between is the Euclidean distance. According to the Euclidean distance formula, the distance between two points in the plane with coordinates (x, y) and (a, b) is given by
dist((x, y), (a, b)) = √(x — a)² + (y — b)²
To visualize this formula, it would look something like this:
For a given value of K the algorithm will find the K nearest neighbors of the data point and then it will assign the class to the data point by having the class which has the highest number of data points out of all classes of the K neighbors.
After computing the distance, the input x gets assigned to the class with the largest probability.
Below is a function named euclidean_distance() that implements this in Python.
#calculating the Euclidean distance between two vectorsdef euclidean_distance(row1, row2): distance = 0.0 for i in range(len(row1)-1): distance += (row1[i] — row2[i])**2 return sqrt(distance)
Minkowski Distance Function
Minkowski distance is a distance measurement between two points in the normed vector space (N dimensional real space) and is a generalization of the Euclidean distance.
Consider two points P1 and P2:
P1: (X1, X2, ..., XN)P2: (Y1, Y2, ..., YN)
Then, the Minkowski distance between P1 and P2 is given as:
When p=2, Minkowski distance is same as Euclidean distance.
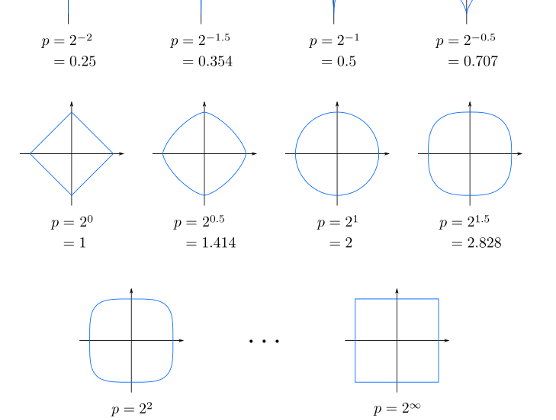
To visualize this formula, it would look something like this:
(When p=2, Minkowski distance is same as Euclidean distance)
To visualize this formula, it would look something like this:
Below is a function named Minkowski_distance() that implements this in Python.
# calculating Minkowski distance between vectorsfrom math import sqrt# calculate Minkowski distancedef Minkowski_distance(a, b, p):return sum(abs(e1-e2)**p for e1, e2 in zip(a,b))**(1/p)# define data row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7]# calculate distance (p=1) dist = Minkowski_distance(row1, row2, 1) print(dist)# calculate distance (p=2) dist = Minkowski_distance(row1, row2, 2) print(dist)
Hamming distance is a metric for comparing two binary data strings. While comparing two binary strings of equal length, Hamming distance is the number of bit positions in which the two bits are different.
The Hamming distance between two strings, a and b is denoted as d(a,b).
In order to calculate the Hamming distance between two strings, and , we perform their XOR operation, (a⊕ b), and then count the total number of 1s in the resultant string.
Suppose there are two strings 11011001 and 10011101.
11011001 ⊕ 10011101 = 01000100. Since, this contains two 1s, the Hamming distance, d(11011001, 10011101) = 2.
Below is a function named hamming_distance() that implements this in Python.
# Return the Hamming distance between string1 and string2.# string1 and string2 should be the same length.
def hamming_distance(string1, string2):
# Start with a distance of zero, and count up
distance = 0
# Loop over the indices of the string
L = len(string1)
for i in range(L):
# Add 1 to distance if these two characters are not equal
if string1[i] != string2[i]:
distance += 1
# Return the final count of differences
return distance
Conclusion
We read about the different distance metric functions that can be used while building a KNN. However, our intuitions, which come from a three-dimensional world, often do not apply in high-dimensional ones. In high dimensions, a different phenomenon arises: the ratio between the nearest and farthest points approaches 1, i.e. the points essentially become uniformly distant from each other. The premise of nearest neighbor search is that “closer” points are more relevant than “farther” points, but if all points are essentially uniformly distant from each other, the distinction is meaningless. To address this issue there we will be looking at some interesting techniques like “Voronoi clustering” in the next article.
