Basics of machine learning: scikit-learn package
We will show here a very basic example of linear regression in the context of curve fitting. This toy example will allow us to illustrate key concepts such as linear models, overfitting, underfitting, regularization, and cross-validation.
We will generate a one-dimensional dataset with a simple model (including some noise), and we will try to fit a function to this data. With this function, we can predict values on new data points. This is a curve-fitting regression problem.
- First, let’s make all the necessary imports:
import numpy as np
import scipy.stats as st
import sklearn.linear_model as lm
import matplotlib.pyplot as plt
%matplotlib inline
2. We now define a deterministic nonlinear function underlying our generative model:
f = lambda x: np.exp(3 * x)
3. We generate the values along the curve on [0,2]:
x_tr = np.linspace(0., 2, 200)
y_tr = f(x_tr)
4. Now, let’s generate data points within [0,1]. We use the function f and we add some Gaussian noise:
x = np.array([0, .1, .2, .5, .8, .9, 1])
y = f(x) + np.random.randn(len(x))
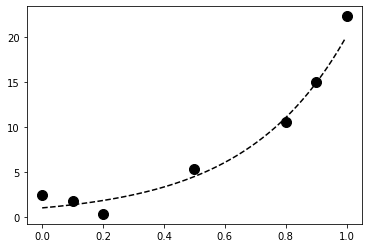
5. Let’s plot our data points on [0,1]:
plt.plot(x_tr[:100], y_tr[:100], '--k')
plt.plot(x, y, 'ok', ms=10)
The dotted curve represents the generative model.
6. Now, we use scikit-learn to fit a linear model to the data. There are three steps. First, we create the model (an instance of the LinearRegression class). Then, we fit the model to our data. Finally, we predict the values from our trained model.
# We create the model.
lr = lm.LinearRegression()
# We train the model on our training dataset.
lr.fit(x[:, np.newaxis], y)
# Now, we predict points with our trained model.
y_lr = lr.predict(x_tr[:, np.newaxis])
We need to convert x and x_tr to column vectors, as it is a general
convention in scikit-learn that observations are rows, while features are
columns. Here, we have seven observations with one feature.
7. We now plot the result of the trained linear model. We obtain a regression line in green here:
plt.plot(x_tr, y_tr, '--k')
plt.plot(x_tr, y_lr, 'g')
plt.plot(x, y, 'ok', ms=10)
plt.xlim(0, 1)
plt.ylim(y.min()-1, y.max()+1)
plt.title("Linear regression")
8.The linear fit is not well-adapted here, as the data points are generated according to a nonlinear model (an exponential curve). Therefore, we are now going to fit a nonlinear model. More precisely, we will fit a polynomial function to our data points. We can still use linear regression for this, by precomputing the exponents of our data points. This is done by generating a Vandermonde matrix, using the np.vander function.
lrp = lm.LinearRegression()
plt.plot(x_tr, y_tr, '--k')
for deg in [2, 5]:
lrp.fit(np.vander(x, deg + 1), y)
y_lrp = lrp.predict(np.vander(x_tr, deg + 1))
plt.plot(x_tr, y_lrp,label='degree ' + str(deg))
plt.legend(loc=2)
plt.xlim(0, 1.4)
plt.ylim(-10, 40)
# Print the model's coefficients.
print(' '.join(['%.2f' % c for c in lrp.coef_]))
plt.plot(x, y, 'ok', ms=10)
plt.title("Linear regression")Out:
17.65 -1.38 0.00
-407.30 990.59 -798.85 246.65 -14.17 0.00
We have fitted two polynomial models of degree 2 and 5. The degree 2 polynomial appears to fit the data points less precisely than the degree 5 polynomial.
However, it seems more robust; the degree 5 polynomial seems really bad at predicting values outside the data points (look for example at the x ≥ 1 portion). This is what we call overfitting; by using a too-complex model, we obtain a better fit on the trained dataset,but a less robust model outside this set.
Note the large coefficients of the degree 5 polynomial; this is generally a sign of overfitting
The scikit-learn API
scikit-learn implements a clean and coherent API for supervised and unsupervised learning. Our data points should be stored in a (N,D) matrix X, where N is the number of observations and D is the number of features. In other words, each row is an observation. The first step in a machine learning task is to define what the matrix X is exactly.
In a supervised learning setup, we also have a target, an N-long vector y with a scalar value for each observation. This value is either continuous or discrete, depending on whether we have a regression or classification problem, respectively.
In scikit-learn, models are implemented in classes that have the fit() and predict() methods. The fit() method accepts the data matrix X as input, and y as well for supervised learning models. This method trains the model on the given data.
The predict() method also takes data points as input (as a (M,D) matrix). It returns the labels or transformed points as predicted by the trained model.
Ordinary least squares regression
Ordinary least squares regression is one of the simplest regression methods. It consists of approaching the output values y i with a linear combination of Xij :
Here, w = (w1 , …, wD ) is the (unknown) parameter vector. Also, ŷ represents the model’s output. We want this vector to match the data points y as closely as possible.
Of course, the exact equality ŷ = y cannot hold in general (there is always some noise and uncertainty — models are always idealizations of reality). Therefore, we want to minimize the difference between these two vectors. The ordinary least squares regression method consists of minimizing the following loss function:
This sum of the components squared is called the L² norm. It is convenient because it leads to differentiable loss functions so that gradients can be computed and common optimization procedures can be performed.
Polynomial interpolation with linear regression
Ordinary least squares regression fits a linear model to the data. The model is linear both in the data points Xi and in the parameters wj . In our example, we obtain a poor fit because the data points were generated according to a nonlinear generative model (an exponential function).
However, we can still use the linear regression method with a model that is linear in w j but nonlinear in xi . To do this, we need to increase the number of dimensions in our dataset by using the basis of polynomial functions. In other words, we consider the following data points:
Here, D is the maximum degree. The input matrix X is therefore the Vandermonde matrix associated to the original data points xi .
Next, we will look how ridge regression works…!!!
