It is expected in this article that you know the basics of how Convolutional Neural Networks work and a good understanding of Deep Learning. If you do not have a good understanding, bookmark this article, and read this article and this one.
Lane Detection is probably one of the most exciting tasks of self-driving cars. This article talks about how I built a lane detection model completely from scratch using the U-Net model and custom loss + metric functions such as the dice coefficient and a focal tversky loss. All the code can be found here. If you would like to contact me, please do contact me on twitter.
The dataset was taken from Thomas Fermi’s “Lane Detection for Carla Driving Simulator” dataset on Kaggle. It was initially created for the Algorithms for Automated Driving course but Fermi had released the dataset on Kaggle. Take a look at the dataset here.
The dataset initially consisted of train and validation folders. The train dataset consisted of 3075 files with the validation set consisting of 129 files. Because of the fact that the model wouldn’t be able to successfully train on this, I used PIL to perform data augmentation via rotating the image in intervals of 5 degrees, horizontal and vertical flips, and I also played around with changing the threshold value. For example, if I had set a value to 150, then every single pixel value that was less than 150 would be set to 0. I was playing around with such augmentation to see how much of a difference would occur when getting rid of such “noise”.
Some of my conclusions were that getting rid of such noise did result in an increase in dice score but the increase was very minimal. The loss went up from 0.8937 (without noise reduction) vs 0.8951. I decided to still go ahead and train the model on data without the “noise reduction technique” as the white lines aren’t consistently at 255.
I made the rotation max of the image 25 degrees. I had left the threshold value as it is. I also did add a validation split of 0.2. After data augmentation, I had generated 23376 training images, 1224 validation images, and 1032 testing images.
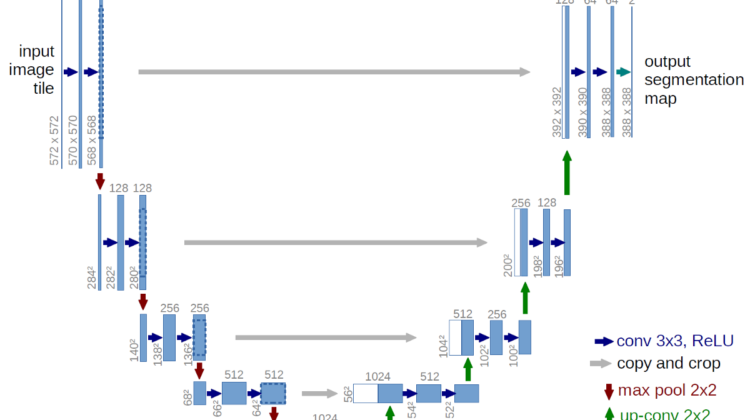
I used the U-Net model created by Ronneberger et al. Created in 2015, the model initially served as a purpose for biomedical image segmentation. The model makes use of skip connections and upsampling via transposed convolutions. It follows an encoder-decoder neural network structure where we pass in an input image and get an output of an image. Take a look at the image below to get a visualization of the model architecture.
Now it probably makes sense to you as to why the model is called the U-Net model. After performing convolutions and downsampling an input image to extract more and more features for the model to learn from, it then upsamples it to generate a new image.
I’d be betting the fact that you have no idea why I’d upsample in the first place and rather not run the model through a basic CNN. The goal of semantic segmentation is to generate a new output image given an input image. Convolutional Neural Networks return an output label for a given image. For example, if I was doing binary classification, I would get an output label of 0 or 1 (or probabilities based on the activation function).
In the case of semantic segmentation, the output of the model should be an image. An image of the model where the lane lines are.
Here’s an example of what the feature and label look like. The input image would be the lane line and the one on the right being the output feature which is another image where the lines are white and everything else is black. This is an example of what our model output should achieve.
This can be achieved through transposed convolutions. When we perform convolutions and downsample the image, we extract features and learn from the image. Now what we want to do is once we extract key features of the input image, we want to generate the output image associated with the input image. This can be done with transposed convolutions.
The gist of transposed convolutions is an input smaller image, we’d perform matrix multiplication of the image on a special kernal. E.g., I’d have a vector of 1 since the smaller image takes in one pixel. We’d then multiply this vector by a kernel (I kept it as 3×3 although you can play around with it) and the output values are now appended to the output image. So if I was given a single pixel of an image, now that pixel vector of 1 becomes a 3×3 matrix. Thus, we’re able to generate 9x the # of pixels just via matrix multiplication using a kernel.
This article, written by Apache MXNet explains transposed convolutions fairly well. Read more at https://medium.com/apache-mxnet/transposed-convolutions-explained-with-ms-excel-52d13030c7e8.
We can also use skip (residual) connections. Skip connections is a method that we can use to avoid the vanishing/exploding gradient problem mainly because of the fact that they flow through the neural network directly without having to go through the non-linear activation functions.
The model learns about features in the first few layers of the U-Net model. When we upsample the image to generate the final output, we would want to store and use that information. If we hadn’t used skip connections, the information the model needs to upsample would’ve gotten lost or would’ve been too abstract for it to be used.
Take a look at https://theaisummer.com/skip-connections/ for a better understanding.
Other solutions do exist such as using Hough transform to detect lane lines. I would assume that alternative solutions would’ve performed somewhat better than the model mainly because of the fact that there isn’t any Machine Learning involved in it. Instead, algorithms such as Hough transform simply segment the image assuming that the location of the lines is in the middle.
I had wanted to play around with augmentation and having lane lines that aren’t in the center of the image which is why I had decided to perform semantic segmentation in this case.
I used both the dice coefficient metric and a custom loss function known as focal tversky loss.
The gist of the dice coefficient loss is that I used was made Milletari et al. in 2016 for 3D medical image segmentation. Read more at https://arxiv.org/pdf/1606.04797.pdf.
pi and gi represent the prediction pixel value and the ground truth. What we’re doing here is that we take the sum of every single time pi = gi and multiply that by 2. That final value is then divided by the sum of the total pixels of both the prediction and ground truth.
The max of the dice score will be between 0 and 1. This allows for a very straightforward way to calculate the loss of the model since we can simply do 1-D (dice coef). I had instead chosen to go with a custom loss function known as the focal tversky loss and use my metric to be dice coefficient instead.
I used a custom variation of the loss function introduced by Abraham et al. (https://arxiv.org/pdf/1810.07842.pdf) that was produced for semantic segmentation. I’m not going to go in-depth into this article because Robin Vinod does a great job explaining it in this article.
I had let the model train for around 20 epochs. The final scores that have gotten is a dice coefficient score of 0.9 and a focal tversky loss score of 0.1. Overall, the model had performed well and I would assume that training it for longer epochs would’ve resulted in higher scores + lower losses.
I also did put this model in CARLAs open-source simulator and tested it. The gif below shows that the model did well but more training could’ve definitely helped in some situations.
Apologies for the low-quality video. Because of the fact that the model was trained on 128×128 images, the images had come out at very low resolution, especially when full-screened.
