Deep reinforcement learning has got to be one of the coolest tools I have used as an engineer. Once finished, all you have to do is tell the agent what it is you want to be accomplished, and watch as the AI figures out incredibly creative ways to accomplish this task.
Understanding neural networks (explained here) is a prerequisite for deep RL. Also, deep reinforcement learning can be more easily understood if you are comfortable with tabulated reinforcement learning, which I explain in-depth here.
Difference between Tabulated RL and Deep RL
A quick summary of tabulated RL is this.
- The agent receives the state from the environment
- Using the ε greedy strategy (or some other state exploration strategy), the agent either does a random action or the agent picks the action that will lead to the state with the highest value
- At the end of the episode, the agent stores all the states that were visited in a table. Then the agent looks back at the states visited in that episode and updates the value of each state based on rewards received
So, if we were given the true values of every state right from the get-go; this would be easy. We just make the agent always move to the state with the highest value. The main issue is finding these correct state values.
What deep RL does is; instead of keeping a table of all the values of each state we encounter, we approximate the value of all the next possible states in real-time using a neural network.
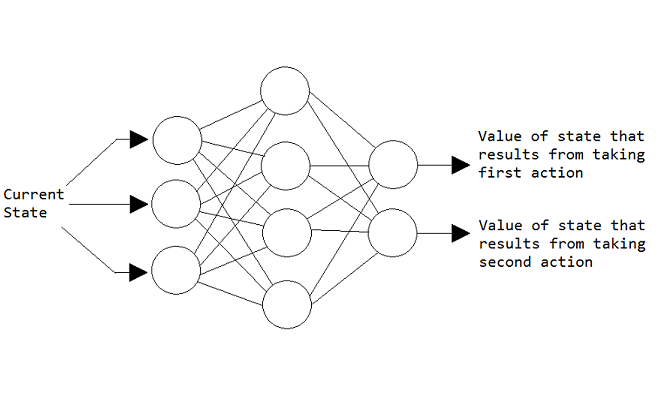
Let’s assume we already have a neural network that we can put our current state into as input and the output will be an array filled with the values of all the next states we can be in (if there is n number of possible actions then typically there are n number of next possible states we can be in). Say our environment is the atari game ‘breakout’, and our agent is in the beginning state (the first frame of the game). In breakout we can do 3 things; stay still, move left, or move right. Each of these actions will bring about a unique new state. We would input our current state into the NN and receive an array telling us the value of the state that will come from taking each action. We then take the action that leads to the highest value.
The diagram below is of a NN in an environment where there are only 2 available actions. The input is the current state, and the output is the next state values.
A quick note on Agent Memory
Before we learn how to train our NN, it’s important to understand how we are storing the information received from playing the game. Most of the time, we are in a state S, we receive reward R, we take action A, we move to the next state S’. I say most of the time because if we are in a terminal state that ends the episode, we just receive a reward R (since there is no next state and action taken).
In practice, what we do is combine these values as a 4-tuple and store them in a list. So, it will look like this.
Now we have this information ready for when we want to train our agent.
Training the Neural Network
So, we know we want our output to be the values of the states that result from taking each action. In order to find all the weights in our NN that will make this possible, we need to identify the loss function we want to minimize. For starters,
We want the difference between the output of our NN and the observed next state values to be 0.
If we use the mean squared error loss function, we obtain:
Now recall from tabulated RL that,
Or the value of the next state is just the reward received in that state + the value of the state after. Now to find V(t+2)true we could keep going and say,
Then find V(t+3)true the same way, then V(t+4)true all the way until we reach a terminal state. But this is impractical and frankly unnecessary.
In practice we can just say:
Or, V(t+1)true = R(t+1) + the highest output we get from inputting the next state, S(t+1), into our NN.
This might seem kind of strange since with an untrained network V(t+2)predicted is going to be inaccurate nonsense. This is true, but over many weight updates the accurate information, R(t+1), is enough to eventually make the V(t+2)predicted values accurate. The way I think about it is this,
But telling the NN R(t+1) lets it improve the accuracy of V(t+1)predicted ever so slightly so that over many iterations the Vpredicted values become accurate.
If what I just said doesn’t make sense, don’t worry about it. Really all you need to know is the loss function that we use is this:
Training on partial information
As a visual, imagine the NN below is in an environment with 2 actions. Now when our agent was in this state, he took action a1, and in the next state receives the reward R(a1,t+1). Now we have no idea what the value of the state that results from taking action a2 is since we took action a1. We need this for training!
What we do is assume that the NN predicted the correct value for this action, so the difference becomes 0. Not very elegant but it works! So, we end up with:
Theoretical Section Summary
The theory can be a bit complicated, depending on how far you want to go into the fine details. The way I learned was by sitting down with some paper and a pencil and manually drawing 3 or 4 of the agent’s timesteps and seeing how I would train these timesteps. If you want a deep understanding of what is going on, I suggest you do the same. Start at state St, where you receive reward Rt. Now draw some made up output values to the NN, then pick an action and record the (S,A,R,S’) tuple in memory. Now do the same for 2 or 3 more timesteps and say you reach a terminal state. Now randomly pick one of these timesteps and try to write down what the loss function would be to train the NN on this timestep. An example of what I did to understand this is shown below:
If all the theory is a bit fuzzy, don’t worry. I would think you were an alien if you understood all of this perfectly the first time ever seeing it. But now that we have been introduced to the theory, the only way to truly learn it is to apply it. Just a side note, my first deep RL project took me weeks to figure out. This project is what taught me how important it is for code to be beautiful and readable. So, don’t be discouraged if you don’t get it right away. If I can do it then so can you.
Soon I will apply this theory to create an agent that plays atari games. The link to this post will be here when finished.
Thank you for reading! If this post helped you in some way or you have a comment or question then please leave a response below and let me know! Also, if you noticed I made a mistake somewhere, or I could’ve explained something more clearly then I would appreciate it if you’d let me know through a response.
