從本篇開始會陸續介紹幾個演算法,或許大家都耳熟能詳,甚至可以說是統計相關的基礎方法。不過,這次要從機器學習的角度來看它們。首先登場的是線性回歸。
根據資料來決定是否發給客戶信用卡,這是一個二元分類問題。如果把問題改成:該給多少信用額度,這就變成一個連續數字的問題了。根據資料來決定多少額度,以機器學習而言,輸入還是資料,輸出從二元分類變成連續性的實數空間。
如何設計這個演算式子呢?我們用加權處理:把每一筆資料乘上權重,並加上常數項d_0,形成
然後追求y和實際y的接近程度。到這一步,其實做的事情和前面PLA很像,差別只在最後沒有取符號,不是只看正負,而是要看確實的數字。因此得到的結果直接輸出就可以了。這叫做線性(回歸)假設。
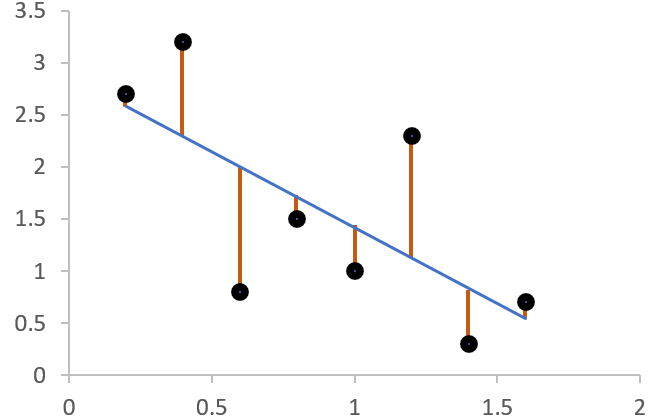
若x為一維資料,則其對應的y可以化成直角坐標,線性假設就是座標上的一條線,而每個資料點實際的y和線性假設的落差(距離)就是垂線。
若x為二維,則此距離變成點到面的垂直距離。
這個垂線距離有一個名稱,叫餘數(residual)。衡量的方法,最簡單就是從小到大評估距離最常用的做法:平方差(squared error)。從機器學習的角度,我們知道評估落差分為in-smaple和out-sample,分別對應E_in和E_out。E_in的寫法為:
應該不用多作解釋吧~
因為h(x)是wx的相乘,如果我們有一串x,就會有一串w,把它們向量化之後,用向量的方式表示上式:
因為兩個一樣形式(shape)的向量相乘,其中一個要轉置不然沒辦法乘。E_out也是一樣的表示方法,但我們在上一篇引入了雜訊的概念,現在y不再是定值,而是有分布的。
VC bound也可以適用在線性回歸,所以可以保證E_in和E_out在資料量N大的時候會接近。現在,要來找找看讓E_in夠小的方法。
首先,把w和x交換一下,式1改成
方便後面整理。式子展開就是(xw-y)^2的相加,可以想成各個向量的長度。這裡要引入範數(norm)的概念,可以把各個向量的長度集合起來變成一個大向量的長度,其成員就是各個向量(xw-y)。改寫成
再把w提出來,所有的x寫成一個X表示由資料輸入組成的向量,所有的y寫成一個y表示由資料的實際答案組成的向量。
因為最開始的時候,我們有加一個常數項,所以x的長度(多項式的項數)是d+1,有N筆。w對應x的長度,所以有d+1筆,其長度為1。y有N筆,長度也是1。這個式子是一個凸函數(convex function),表示E_in對w做圖會得到一個像山谷的曲線,如下:
不要問我為什麼是凸函數,這個要另外證明~但顯而易見的是,這個曲線有最小值,其導數為0。什麼導數?E_in對w偏微分的導數。
到這個點,就是最小值,找不到更低的了。所以改成把式2偏微分。先把式2寫成
其實就是展開。然後把x^Tx寫成矩陣A((d+1)×(d+1)),x^Ty寫成向量b((d+1)×1),y^Ty寫成常數c(1)。上式改為
若w為一維,上式為一元二次方程式,微分結果就是
但w是向量,所以要寫成
然後把A、b換回原本的表示式
x、y都是已知,此式變為一次式。在這裡,為了求廣義解,我們使用線性代數裡pseudo-inverse(x-dag)來解:
因求梯度最小值,設梯度為0,移項之後再乘上(X^TX)^(-1),可得
其中
為pseudo-inverse矩陣(左逆矩陣)。這樣無論(X^TX)是否存有反矩陣都可以使用。通常在程式裡都已經有寫好的package,所以不用執著怎麼計算。
回顧一下線性回歸的演算法流程吧:
- 將資料建為X、y矩陣,其中X為N×(d+1)維,y為N×1維。
2. 計算pseudo-inverse矩陣(x-dag),其維度為(d+1)×N。
3. 公式解w=(x-dag)y。
乍看之下好像有點爭議。
說不算的應該是覺得它沒有神秘感:公式解、一步到位,沒有漸進學習,慢慢進步的感覺。但說它算也有道理,因為它有好的E_in、E_out,而且尋找pseudo-inverse的過程中,要不是程式寫好package,可也是要一步步找的呀。這過程總不能因為程式幫忙做了就不算吧?
其實,只要有找到好的E_out,則不管花了多少成本,是多是少,學習的過程就是有發生。
現在換個想法好了。我們能不能用VC bound以外的角度來看線性回歸能得到好的E_out的方法呢?
Learning curve
每次抽樣都會得到一個E_in,所以可以假設一個E_in的平均值,為多次抽樣之後平均的結果。先講結論:此值為
等一下會推導這個式子,不過不會用太嚴謹的方式,主要是知道精神就好。根據這個式子,可以知道E_in的平均和noise level以及(d+1)/N有關。
- noise level指雜訊量。因為y變成一種分布,而不再是單一定值,即使是target function也有抓不到y的時候。這些y就是雜訊。
- 比雜訊量低(d+1)/N就是要證明的。d+1是資料的維度,也是權重(w)的數目。N是資料量。
回到線性回歸的E_in,其定義為
y-hat為預測值。可以換成wx,而w可以用x-dag來代替,所以可以改寫為
把y提出來,得到
其中x(x-dag)又稱為hat matrix,因為y乘上它之後就變成y-hat,長出帽子了。接著來看看hat matrix的幾何意義:
y是一個N維空間的向量,y-hat是wx相乘,而x是一筆筆資料堆起來的,是一個欄向量(行向量,column vector),只有一行。w和裡面的元素相乘,可以視為w將x的元素做線性組合,構成另一個向量空間,這個空間的維度是d+1。這個向量空間隨著w調整,就可以產生不同的y-hat,而最佳解w_LIN產生的y-hat也在其中。
線性回歸追求最小的餘數,即y-(y-hat)。在這裡,其實就是垂線距離,y-(y-hat)在最小距離時垂直於wx的向量空間。故hat matrix就是投影,把y投影到wx的向量空間產生y-hat,y-(y-hat)就是(I-hat matrix)。原本的y有N維度,wx空間只有d+1維度,所以y-(y-hat)的維度就是N-(d+1)。維度就是空間的自由度。
若現在有一個y,其target function在wx的向量空間裡,如圖:
因為y可以看成target function+雜訊,如果target function已經在向量空間裡,餘數只要處理雜訊部分就好。一樣把雜訊投影到向量空間:
因為target function已經在向量空間裡,所以是沒有垂線距離的。只剩下雜訊的部分有。如果把E_in平均,然後把noise範數的平均叫noise level,則上式變成
[N-(d+1)]/N就是(1-(d+1)/N)。也就是最開始的式子。
同時,E_out的平均也可以證明(手法複雜許多,這裡先略過)得到其值為
長得很像。兩者都有資料量N這個變數,我們把他們分別對資料量作圖:
一個是1-(d+1)/N,一個是1+(d+1)/N,所以在資料小的時候,E_out很大,而E_in很小。隨著資料量增加,後面那一項越來越小,可以預期雙方最後都會趨近noise level,也就是σ²。σ是雜訊,而平方是因為前面的式子裡提到的範數。E_in和E_out不會完全相遇,他們的落差為
比較一下VC bound的限制為
不太一樣,因為VC bound談的是最差的狀況,而這邊談的是平均值。不過可以確定的是:資料量越大,他們都會越小。
既然E_in和E_out之間的落差可以收斂,這就符合機器學習的條件。我們可以說:線性回歸是一種機器學習。
比較一下線性回歸和線性分類的差異:
- 線性分類:y為+1/-1,h(x)為sign(w^Tx),error是看兩者符號是否相同。資料必須線性可分,但即使如此,根據情況也可能需要花不少時間。
- 線性回歸:y屬於整個實數空間,不用限定,h(x)直接輸出,不必取符號;error直接看兩者差距。有pseudo-inverse,可以很快找到解。
能不能用線性回歸來做線性分類的事情?例如我先用線性回歸尋找w,然後再用w^Tx取符號,馬上歸類好。聽起來很有道理,但能用更數學一點的角度解釋嗎?
如果我們把線性分類和線性回歸的error作圖,畫在同一張上面。y=1時兩個error分別是這樣:
紅色線是線性回歸的error,因為是一個二次式。藍線是線性分類的error,折線處w^Tx=0。紅線的值全部都在藍線上方。
再看看y=-1的時候:
一樣,紅線值都在藍線上方。這表示線性回歸的y值≥線性分類的y值。根據VC bound:線性分類的E_out<線性分類的E_in(+根號內一串式子,詳情請見系列(4))。而根據上圖,線性分類的E_in<線性回歸的E_in,所以可以把上式代換為線性分類的E_out<線性回歸的E_in。這樣,只要把線性回歸的E_in找好(夠小),線性分類的E_out也能做好(夠小)。這就是數學上的解釋。
所以,可以用線性回歸來處理線性分類的問題,或者是把它當作線性分類/pocket演算法的初始w,讓我們進一步在尋找更精確的w之前可以快速有個方向。
本篇介紹線性回歸。下一篇會介紹另一個經典演算法和機器學習之間的關係,敬請期待。
