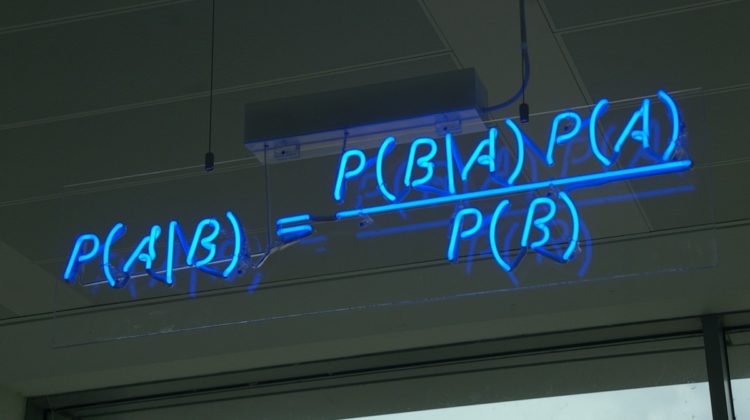
It has more than two centuries but has become the most used Machine Learning algorithms
Bayes Theorem allows anyone, in a deceptively simple manner, to calculate a conditional probability where intuition often fails. You’ve might bump into this theorem in Machine Learning when dealing with Maximum a Posteriori (MAP) — a probability framework for fitting a model to a training dataset — or in classification predictive modeling problems such as the Bayes Optimal Classifier and Naive Bayes.
History of Bayes Theorem
Reverend Thomas Bayes was a wealthy presbyterian minister and amateur mathematician who lived in London in the eighteenth-century. Without realizing it created, the reverend created a completely new religion that influenced a great number of study fields over decades. Europe was living in a very religious controversial era. Scientists were trying to make use of evidence around us to come up with rational conclusions about God.
It is unknown if Bayes wanted to prove the existence of God, but it is historically proven that Bayes wanted to mathematically deal with the issue of cause and effect, which ended in his theorem.
Bayes did not believe his theorem enough to publish it…
So he files his observations and conclusions in the archives and dies 10–15 years later. Richard Price, a friend of Bayes and also a presbyterian minister and amateur mathematician, goes through such archives and finds this theorem. In opposite to Bayes, Price was a more renowned minister and he decides that the theorem will help to prove the existence of God. He publishes Bayes’ study but it does not get the expected attention, since it was published in a journal whose readers were not mostly mathematicians, and thus little attention was given to the topic.
In 1774 when almost 100 years had already passed since Bayes created his theorem, as a young man of 25 Pierre-Simon de Laplace discovers this theorem and calls it the Probability of Causes. Contrary to Bayes, Laplace went on to being of the world’s most renowned mathematicians to this day and he spent 25 years of his life developing Bayes’s rule into the mathematical equation we know today.
Bayes’ Rule
As discussed, Bayes Theorem is a mathematical rule for determining conditional probability, which is the likelihood of an outcome occurring, based on a previous outcome occurring.
Let’s check the terms that compose the equation…
- P(A|B) — it’s the posterior probability. The probability of occurring A knowing the evidence B
- P(A) — Prior probability
- P(B|A) — Likelihood
- P(B) — Evidence
- Thus,
Posterior = Likelihood * Prior / Evidence
Let’s consider the following… You want to talk your sweetheart out for a picnic. You’ve checked the weather report and it announces sunny day. However, when you look out the window there are threatening clouds… Will it rain and ruin the picnic?
Let’s try to use Bayes Theorem to figure out…
So, what do we know about cloudy days?
- 50% of all rainy days start off cloudy!
- 40% of days start cloudy
- 10% of days in July are rainy
Therefore, what’s the probability that it will rain during the day knowing we have a cloudy morning? Taking Bayes theorem equation:
P (Rain | Cloud) = (P(Rain) * P(Cloud|Rain)) / P(Cloud)
- P(Rain) — Probability of rain in July = 10%
- P(Cloud|Rain) — Probability of a cloudy day, knowing the day started cloudy = 50%
- P(Cloud) — Probability of day starting cloudy = 40%
P(Rain|Cloud) = 0.1 x 0.50.4 = .125
It seems there’s only a 12.5% chance of rain! So, let’s risk it and go for a picnic!
