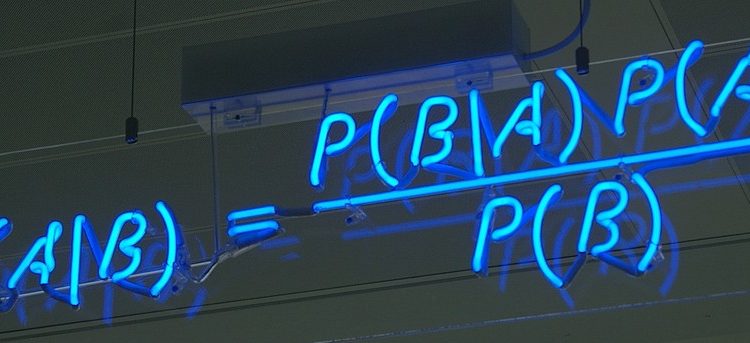
The concept of Bayesian is something that just crashed into my life when I got into college that always confused me and never really got to grasp the whole of it. I happen to be able to only fully digest the Frequentist view of the world and as I was studying the Bayesian theorem and Bayesian Linear Regression, I found it very difficult to comprehend fully. This post will go through struggles I’ve had in understanding the Bayesian point of view and clear up some vague ideas about it. Also, I’ve implemented the whole process in Google Colab for anyone who wants to follow through in practice.
Frequentist Probability vs Bayesian Probability
I think the examples of explaining the frequentist view by a coin toss or dice roll only makes it more confusing. Frequentist probability is just a simple calculation of how frequently did an event happened.
Bayesian probability, however, gives how confident we can tell about a certain event happening with evidence. In other words, knowing how confident we can say about such an event happening can also be implied from knowing the uncertainty of the event.
Let’s say, there’s a 50% chance of head from a coin toss. Frequentists say that there can be 50 times head out of 100. Rather, Bayesians say that the confidence of a head is 50% when a coin is tossed.
Instead of understanding Bayes’ theorem as a simple extension of a conditional probability, I think it’s easier to comprehend it in a way that it defines the relational confidence of an event before and after something (evidence) happened. Therefore, the uncertainty of an event decreases accordingly as it happens more and more. Also, the hypothesis can be interpreted as our belief in what we are trying to observe.
Linear regression that we are familiar with is just a simple fitting of coefficients in an equation to minimize the residual error to the target equation. Also the same concept in finding the optimal weight vector to fit the prediction data to the target data in machine learning.
Assuming there is a linear correlation between target value y and attributes of x, we can predict an expected value out of any given data with the fitted weight vector β. To successfully “fit” the weight vector to obtain a reasonable prediction from unknown data, we normally use Mean-Squared-Error (MSE) as given below:
In matrix form, we can represent it as below:
Therefore, its’ gradient with respect to β:
Which gives us our optimum weight vector:
As we briefly went over the Bayes’ theorem, this concept of conditional probability extends to the Bayesian linear regression problem. Before we dive into this, it’s best to straighten out some related terms. We will define prior, likelihood, and posterior distributions with respect to the weight vector w and given target data t. As we make assumptions on what our distributions will be like in w as prior and t as the likelihood, we can find the posterior distribution of w given t. Then, we will look at the posterior predictive distribution to make actual predictions from new incoming data.
Prior Distribution
This is our prior belief on the weight vector’s distribution which we will refer to the parameter as w below (same as β above):
We will assume that the parameter w follows the Gaussian distribution with a mean of m₀ and a covariance of S₀.
Likelihood
Our likelihood function is a conditional probability of target data t on input data X, w, and β. Assume that the noise ϵ follows Gaussian distribution with zero mean and precision (inverse of variance β), our joint conditional probability can be formulated as below:
Posterior Distribution
Since posterior distribution is the product of likelihood and the prior distribution, it also follows a Gaussian distribution.
I couldn’t find the detailed derivations for the mean and the covariance above, but it could be simply put in as below:
There is no need to differentiate to find the solution w corresponding to the maximum value of the posterior distribution in our case since Maximum A Posteriori (MAP) for the Gaussian is equal to the mean.
Therefore, if we consider a prior distribution as below:
Then, our posterior distribution’s parameters become simplified as below:
Also, the log posterior is as follows which implies that maximizing the log posterior with respect to w is equivalent to minimizing the MSE error just like the linear regression above:
Conjugate Prior Distribution
The term conjugate was always confusing for me, but it just means that they come from the same distribution family which is Gaussian for our case. The definition from Wikipedia is as follows:
In Bayesian probability theory, if the posterior distributions p(θ | x) are in the same probability distribution family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood function p(x | θ).
Posterior Predictive Distribution
In practice, we often make predictions on the expected value t from new input data x more than w. Predictive distribution with respect to t is defined as below:
Evidence Function
From the Bayes’ theorem, we can define the relationship between each term as below:
Evidence function, also known as the marginal likelihood function, with respect to t given α and β is obtained as below:
We’ve already defined the related terms at the likelihood and the prior which results in the form as follows:
This comes down to the log marginal likelihood in the form as below:
Evidence Maximization
Evidence maximization is the process of finding the most probable hyper-parameters α and β on training data t. Maximizing the log marginal likelihood is considered with respect to α and β separately. First, for the covariance S, we should define the eigenvector equation as below:
Then, the derivative of the log marginal likelihood with respect to α becomes as below:
The derivative with respect to β is as follows:
In my opinion, Bayesian linear regression is such a neat way of analyzing the data with statistical techniques. The whole process of making predictions with uncertainty and even finding the optimal hyper-parameters felt very well-structured to me. I still couldn’t understand the whole mathematical derivations behind each component, but the correlation of each probability distribution and meaning of them became clear by writing this article.
In summary, the prior distribution is our belief or assumption on the weight vector with mean and covariance. Then, the likelihood which is the probability distribution of the target data can be calculated given input data, weight vector, and variance of error. Finally, the posterior distribution with respect to weight vector given target data can be obtained by mathematical derivations and posterior predictive distribution is just a simple calculation of expected value out of new incoming data using obtained mean and covariance from the posterior distribution. In addition, pre-defined hyper-parameters such as variances or degree of a polynomial basis function can be obtained through the process of evidence maximization.
Thank you very much for reading this and hope this could help anyone whose going through the same struggles as I did. I’m open to any comments or discussion, so please leave a note if you have any!
[1] Martin Krasser, Bayesian regression with linear basis function models, 2019
[2] Kiho Hong, Bayesian Linear Regression, 2016
[3] Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006
