Bias – “When your test data has a different distribution than your training data. for example: you train your model to detect vehicles during day time and for testing, you try to detect vehicles during night time.” — from Sindhu, Slack
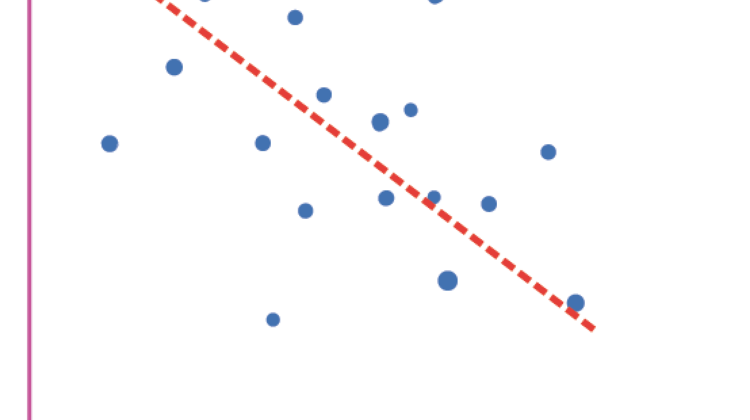
Bias refers to the difference between your model’s expected predictions and the actual values it produces. It occurs when the learning model is unable to truly capture the relationship between the features and the target data. Check out the linear regression in diagram 1. No matter how many points of data you give your model, the linear regression algorithm won’t be able to give a very accurate output. This is a low complexity model and it means that underfitting will often occur.
Machine learning models that have high bias include logistic and linear regression (quite simple models) and they often under-fit the data, whereas models such as Support Vector Machines and Decision trees have low bias (and are quite complex). They often over-fit the data.
Bias can be reduced by doing any of the following:
- Change the model. If your data doesn’t have a linear relationship, don’t use a linear model.
- Balance the training data. Sometimes the training data does not represent all of the groups or outcomes. Bias needs to be balanced with variance.
- Tweak the hyper-parameters.
Variance refers to the effects of when models make too complex of an assumption. They fit the model too closely to the data (overfit). Although overfitting makes the model accurate with the training data, it does not translate to a good predictive model, i.e. it does not work well with the testing data. Such a fit captures all of the noise and features which should be ignored, or whose influence on the model should be minimal. See Diagram 2 for an example of this.
So, if your model gives high accuracy on training, but works poorly on testing, the model has too close of a fit.
Do one of the following to reduce the error:
- Use ensemble learning, i.e. training using multiple models. Ensemble learning takes advantage of both weak and strong learners to improve predictions.
- Add more data, which will increase the data/noise ratio. When more data is supplied, a model can come up with better general rules, which will also apply to the new data.
Unfortunately, you can never get rid of all of the bias and all of the variance. The best that can be done is to find a balance that will give you the least amount of error.
Prediction error = Bias error + Variance error + Irreducible error
If the target is Y, and x is our features, we can think of the error as:
Y = f(x) + e
The error is the same as the difference between the predicted value and the real value.
As a simple summary:
* Bias can be thought of as over-simplified model assumptions (like our linear regression), and
* Variance can be thought of as over-complicated assumptions.
- https://medium.com/swlh/the-bias-variance-tradeoff-f24253c0ab45
2. https://stackabuse.com/introduction-to-neural-networks-with-scikit-learn/
