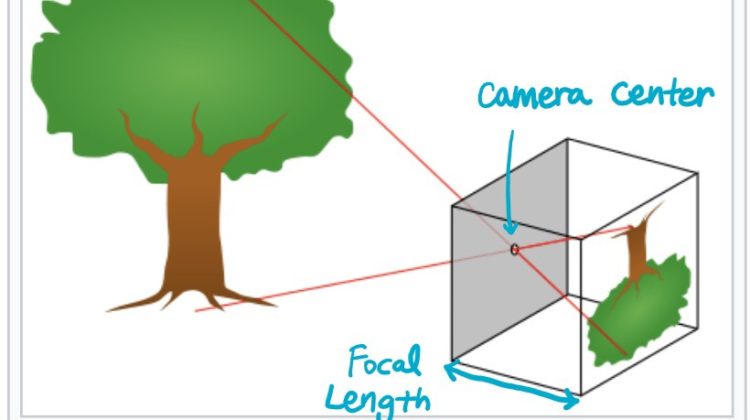
Now we can frame the projection problem (World Coordinates → Image Coordinates) as
- World coordinates → Camera coordinates
- Camera coordinates → Image coordinate
Oworld [Xw,Yw,Zw] → Oimage [u,v]
How? by using Linear Algebra!
1. World coordinates → Camera coordinatesOcamera = [R|t] * Oworld2. Camera coordinates → Image coordinateOimage = K * Ocamera Remind me what K (camera intrinsic parameter) was?
Both steps 1 and 2 are just matrix multiplications. Therefore it can be re-written (combined) as:
Oimage = P * Oworld = K[R|t] * OworldLet P = K[R|t]
P as Projection
Wait, K is (3,3) matrix. [R|t] is (3,4). (| means you are concatenating matrix R with vector t.) Oworld [Xw,Yw,Zw] is (3,1).
Then you can’t multiply K[R|t] (3,4) with Oworld [Xw,Yw,Zw] (3,1)!
😎 We can resolve this by adding one at the end the Oworld vector [Xw,Yw,Zw,1], called homogeneous coordinate (or projective coordinate).
