Gradient descent is an optimization algorithm that follows the negative gradient of an objective function in order to locate the minimum of the function.
A limitation of gradient descent is that a single step size (learning rate) is used for all input variables. Extensions to gradient descent like AdaGrad and RMSProp update the algorithm to use a separate step size for each input variable but may result in a step size that rapidly decreases to very small values.
The Adaptive Movement Estimation algorithm, or Adam for short, is an extension to gradient descent and a natural successor to techniques like AdaGrad and RMSProp that automatically adapts a learning rate for each input variable for the objective function and further smooths the search process by using an exponentially decreasing moving average of the gradient to make updates to variables.
In this tutorial, you will discover how to develop gradient descent with Adam optimization algorithm from scratch.
After completing this tutorial, you will know:
- Gradient descent is an optimization algorithm that uses the gradient of the objective function to navigate the search space.
- Gradient descent can be updated to use an automatically adaptive step size for each input variable using a decaying average of partial derivatives, called Adam.
- How to implement the Adam optimization algorithm from scratch and apply it to an objective function and evaluate the results.
Let’s get started.

Gradient Descent Optimization With Adam From Scratch
Photo by Don Graham, some rights reserved.
Tutorial Overview
This tutorial is divided into three parts; they are:
- Gradient Descent
- Adam Optimization Algorithm
- Gradient Descent With Adam
- Two-Dimensional Test Problem
- Gradient Descent Optimization With Adam
- Visualization of Adam
Gradient Descent
Gradient descent is an optimization algorithm.
It is technically referred to as a first-order optimization algorithm as it explicitly makes use of the first-order derivative of the target objective function.
- First-order methods rely on gradient information to help direct the search for a minimum …
— Page 69, Algorithms for Optimization, 2019.
The first-order derivative, or simply the “derivative,” is the rate of change or slope of the target function at a specific point, e.g. for a specific input.
If the target function takes multiple input variables, it is referred to as a multivariate function and the input variables can be thought of as a vector. In turn, the derivative of a multivariate target function may also be taken as a vector and is referred to generally as the gradient.
- Gradient: First-order derivative for a multivariate objective function.
The derivative or the gradient points in the direction of the steepest ascent of the target function for a specific input.
Gradient descent refers to a minimization optimization algorithm that follows the negative of the gradient downhill of the target function to locate the minimum of the function.
The gradient descent algorithm requires a target function that is being optimized and the derivative function for the objective function. The target function f() returns a score for a given set of inputs, and the derivative function f'() gives the derivative of the target function for a given set of inputs.
The gradient descent algorithm requires a starting point (x) in the problem, such as a randomly selected point in the input space.
The derivative is then calculated and a step is taken in the input space that is expected to result in a downhill movement in the target function, assuming we are minimizing the target function.
A downhill movement is made by first calculating how far to move in the input space, calculated as the step size (called alpha or the learning rate) multiplied by the gradient. This is then subtracted from the current point, ensuring we move against the gradient, or down the target function.
- x(t) = x(t-1) – step_size * f'(x(t-1))
The steeper the objective function at a given point, the larger the magnitude of the gradient and, in turn, the larger the step taken in the search space. The size of the step taken is scaled using a step size hyperparameter.
- Step Size (alpha): Hyperparameter that controls how far to move in the search space against the gradient each iteration of the algorithm.
If the step size is too small, the movement in the search space will be small and the search will take a long time. If the step size is too large, the search may bounce around the search space and skip over the optima.
Now that we are familiar with the gradient descent optimization algorithm, let’s take a look at the Adam algorithm.
Adam Optimization Algorithm
Adaptive Movement Estimation algorithm, or Adam for short, is an extension to the gradient descent optimization algorithm.
The algorithm was described in the 2014 paper by Diederik Kingma and Jimmy Lei Ba titled “Adam: A Method for Stochastic Optimization.”
Adam is designed to accelerate the optimization process, e.g. decrease the number of function evaluations required to reach the optima, or to improve the capability of the optimization algorithm, e.g. result in a better final result.
This is achieved by calculating a step size for each input parameter that is being optimized. Importantly, each step size is automatically adapted throughput the search process based on the gradients (partial derivatives) encountered for each variable.
We propose Adam, a method for efficient stochastic optimization that only requires first-order gradients with little memory requirement. The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients; the name Adam is derived from adaptive moment estimation
— Adam: A Method for Stochastic Optimization
This involves maintaining a first and second moment of the gradient, e.g. an exponentially decaying mean gradient (first moment) and variance (second moment) for each input variable.
The moving averages themselves are estimates of the 1st moment (the mean) and the 2nd raw moment (the uncentered variance) of the gradient.
— Adam: A Method for Stochastic Optimization
Let’s step through each element of the algorithm.
First, we must maintain a moment vector and exponentially weighted infinity norm for each parameter being optimized as part of the search, referred to as m and v (really the Greek letter nu) respectively. They are initialized to 0.0 at the start of the search.
The algorithm is executed iteratively over time t starting at t=1, and each iteration involves calculating a new set of parameter values x, e.g. going from x(t-1) to x(t).
It is perhaps easy to understand the algorithm if we focus on updating one parameter, which generalizes to updating all parameters via vector operations.
First, the gradient (partial derivatives) are calculated for the current time step.
Next, the first moment is updated using the gradient and a hyperparameter beta1.
- m(t) = beta1 * m(t-1) + (1 – beta1) * g(t)
Then the second moment is updated using the squared gradient and a hyperparameter beta2.
- v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2
The first and second moments are biased because they are initialized with zero values.
… these moving averages are initialized as (vectors of) 0’s, leading to moment estimates that are biased towards zero, especially during the initial timesteps, and especially when the decay rates are small (i.e. the betas are close to 1). The good news is that this initialization bias can be easily counteracted, resulting in bias-corrected estimates …
— Adam: A Method for Stochastic Optimization
Next the first and second moments are bias-corrected, starring with the first moment:
- mhat(t) = m(t) / (1 – beta1(t))
And then the second moment:
- vhat(t) = v(t) / (1 – beta2(t))
Note, beta1(t) and beta2(t) refer to the beta1 and beta2 hyperparameters that are decayed on a schedule over the iterations of the algorithm. A static decay schedule can be used, although the paper recommend the following:
- beta1(t) = beta1^t
- beta2(t) = beta2^t
Finally, we can calculate the value for the parameter for this iteration.
- x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + eps
Where alpha is the step size hyperparameter, eps is a small value (epsilon) such as 1e-8 that ensures we do not encounter a divide by zero error, and sqrt() is the square root function.
Note, a more efficient reordering of the update rule listed in the paper can be used:
- alpha(t) = alpha * sqrt(1 – beta2(t)) / (1 – beta1(t))
- x(t) = x(t-1) – alpha(t) * m(t) / (sqrt(v(t)) + eps)
To review, there are three hyperparameters for the algorithm, they are:
- alpha: Initial step size (learning rate), a typical value is 0.001.
- beta1: Decay factor for first momentum, a typical value is 0.9.
- beta2: Decay factor for infinity norm, a typical value is 0.999.
And that’s it.
For full derivation of the Adam algorithm in the context of the Adam algorithm, I recommend reading the paper.
Next, let’s look at how we might implement the algorithm from scratch in Python.
Gradient Descent With Adam
In this section, we will explore how to implement the gradient descent optimization algorithm with Adam.
Two-Dimensional Test Problem
First, let’s define an optimization function.
We will use a simple two-dimensional function that squares the input of each dimension and define the range of valid inputs from -1.0 to 1.0.
The objective() function below implements this function
|
# objective function def objective(x, y): return x**2.0 + y**2.0 |
We can create a three-dimensional plot of the dataset to get a feeling for the curvature of the response surface.
The complete example of plotting the objective function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 3d plot of the test function from numpy import arange from numpy import meshgrid from matplotlib import pyplot
# objective function def objective(x, y): return x**2.0 + y**2.0
# define range for input r_min, r_max = –1.0, 1.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection=‘3d’) axis.plot_surface(x, y, results, cmap=‘jet’) # show the plot pyplot.show() |
Running the example creates a three-dimensional surface plot of the objective function.
We can see the familiar bowl shape with the global minima at f(0, 0) = 0.
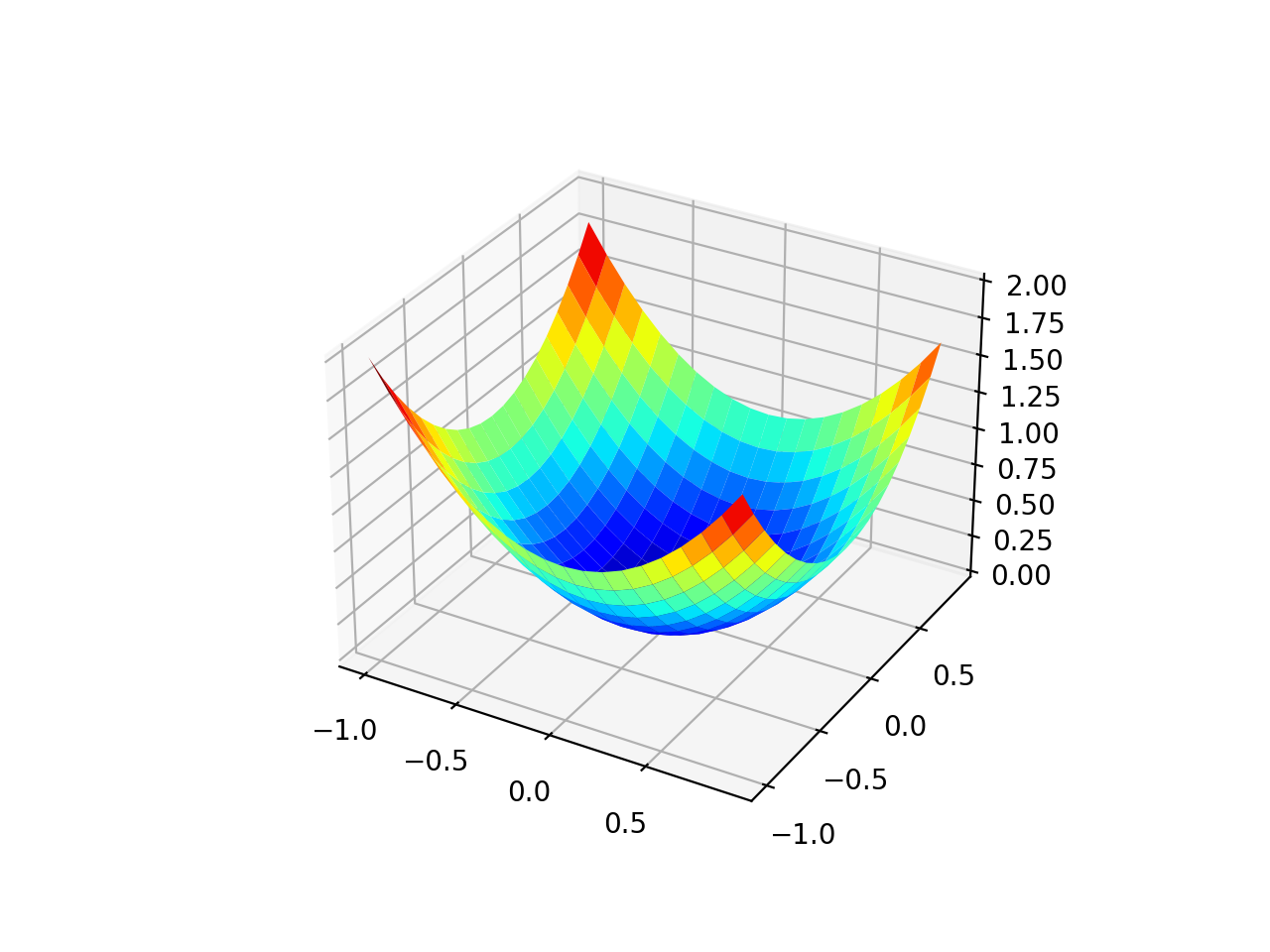
Three-Dimensional Plot of the Test Objective Function
We can also create a two-dimensional plot of the function. This will be helpful later when we want to plot the progress of the search.
The example below creates a contour plot of the objective function.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# contour plot of the test function from numpy import asarray from numpy import arange from numpy import meshgrid from matplotlib import pyplot
# objective function def objective(x, y): return x**2.0 + y**2.0
# define range for input bounds = asarray([[–1.0, 1.0], [–1.0, 1.0]]) # sample input range uniformly at 0.1 increments xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(x, y, results, levels=50, cmap=‘jet’) # show the plot pyplot.show() |
Running the example creates a two-dimensional contour plot of the objective function.
We can see the bowl shape compressed to contours shown with a color gradient. We will use this plot to plot the specific points explored during the progress of the search.
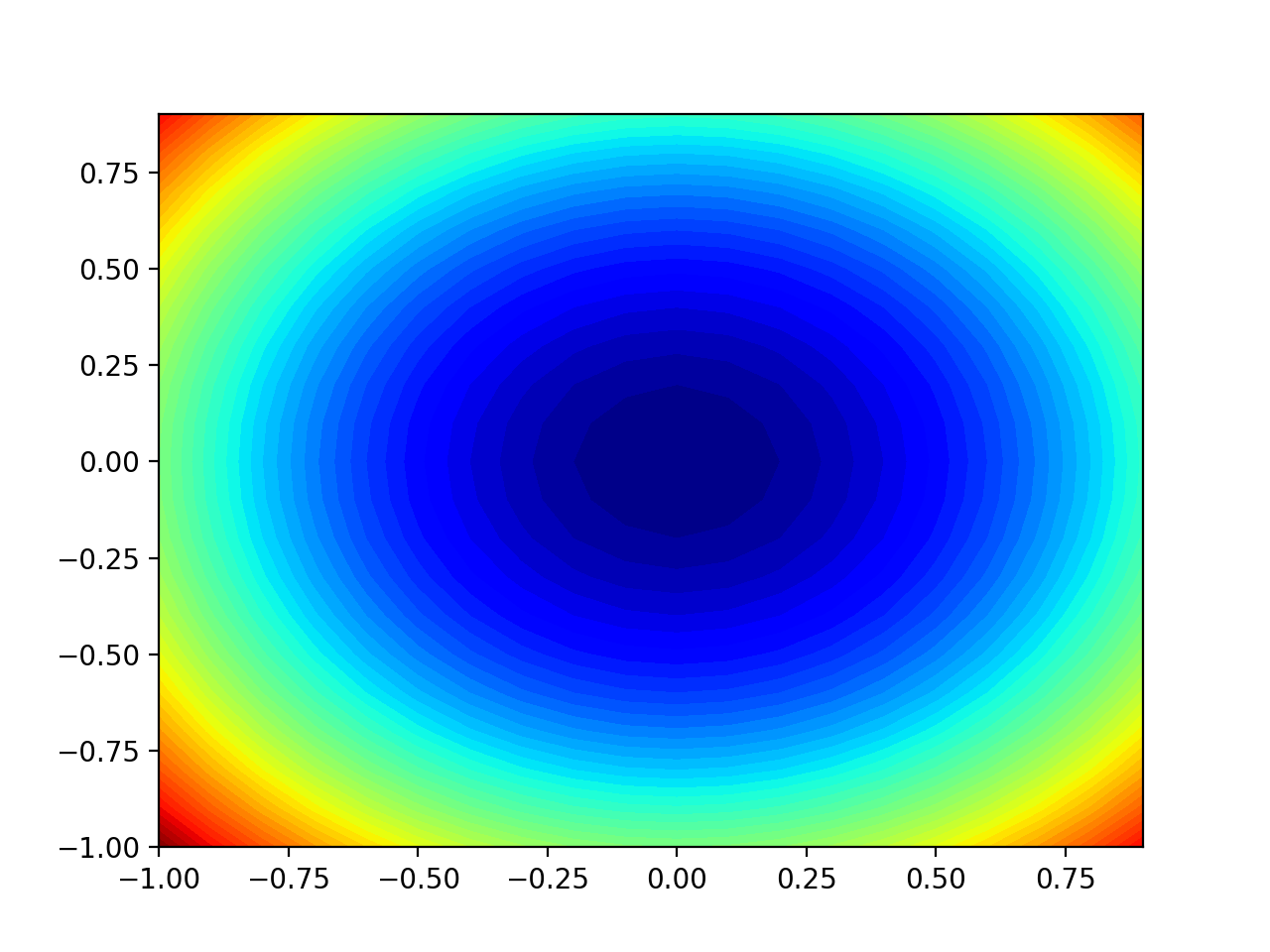
Two-Dimensional Contour Plot of the Test Objective Function
Now that we have a test objective function, let’s look at how we might implement the Adam optimization algorithm.
Gradient Descent Optimization With Adam
We can apply the gradient descent with Adam to the test problem.
First, we need a function that calculates the derivative for this function.
The derivative of x^2 is x * 2 in each dimension. The derivative() function implements this below.
|
# derivative of objective function def derivative(x, y): return asarray([x * 2.0, y * 2.0]) |
Next, we can implement gradient descent optimization.
First, we can select a random point in the bounds of the problem as a starting point for the search.
This assumes we have an array that defines the bounds of the search with one row for each dimension and the first column defines the minimum and the second column defines the maximum of the dimension.
|
... # generate an initial point x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0]) score = objective(x[0], x[1]) |
Next, we need to initialize the first and second moments to zero.
|
... # initialize first and second moments m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] |
We then run a fixed number of iterations of the algorithm defined by the “n_iter” hyperparameter.
|
... # run iterations of gradient descent for t in range(n_iter): ... |
The first step is to calculate the gradient for the current solution using the derivative() function.
|
... # calculate gradient gradient = derivative(solution[0], solution[1]) |
The first step is to calculate the derivative for the current set of parameters.
|
... # calculate gradient g(t) g = derivative(x[0], x[1]) |
Next, we need to perform the Adam update calculations. We will perform these calculations one variable at a time using an imperative programming style for readability.
In practice, I recommend using NumPy vector operations for efficiency.
|
... # build a solution one variable at a time for i in range(x.shape[0]): ... |
First, we need to calculate the moment.
|
... # m(t) = beta1 * m(t-1) + (1 – beta1) * g(t) m[i] = beta1 * m[i] + (1.0 – beta1) * g[i] |
Then the second moment.
|
... # v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 – beta2) * g[i]**2 |
Then the bias correction for the first and second moments.
|
... # mhat(t) = m(t) / (1 – beta1(t)) mhat = m[i] / (1.0 – beta1**(t+1)) # vhat(t) = v(t) / (1 – beta2(t)) vhat = v[i] / (1.0 – beta2**(t+1)) |
Then finally the updated variable value.
|
... # x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + eps x[i] = x[i] – alpha * mhat / (sqrt(vhat) + eps) |
This is then repeated for each parameter that is being optimized.
At the end of the iteration we can evaluate the new parameter values and report the performance of the search.
|
... # evaluate candidate point score = objective(x[0], x[1]) # report progress print(‘>%d f(%s) = %.5f’ % (t, x, score)) |
We can tie all of this together into a function named adam() that takes the names of the objective and derivative functions as well as the algorithm hyperparameters, and returns the best solution found at the end of the search and its evaluation.
This complete function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# gradient descent algorithm with adam def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e–8): # generate an initial point x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0]) score = objective(x[0], x[1]) # initialize first and second moments m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # run the gradient descent updates for t in range(n_iter): # calculate gradient g(t) g = derivative(x[0], x[1]) # build a solution one variable at a time for i in range(x.shape[0]): # m(t) = beta1 * m(t-1) + (1 – beta1) * g(t) m[i] = beta1 * m[i] + (1.0 – beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 – beta2) * g[i]**2 # mhat(t) = m(t) / (1 – beta1(t)) mhat = m[i] / (1.0 – beta1**(t+1)) # vhat(t) = v(t) / (1 – beta2(t)) vhat = v[i] / (1.0 – beta2**(t+1)) # x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + eps x[i] = x[i] – alpha * mhat / (sqrt(vhat) + eps) # evaluate candidate point score = objective(x[0], x[1]) # report progress print(‘>%d f(%s) = %.5f’ % (t, x, score)) return [x, score] |
Note: we have intentionally used lists and imperative coding style instead of vectorized operations for readability. Feel free to adapt the implementation to a vectorized implementation with NumPy arrays for better performance.
We can then define our hyperparameters and call the adam() function to optimize our test objective function.
In this case, we will use 60 iterations of the algorithm with an initial steps size of 0.02 and beta1 and beta2 values of 0.8 and 0.999 respectively. These hyperparameter values were found after a little trial and error.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
... # seed the pseudo random number generator seed(1) # define range for input bounds = asarray([[–1.0, 1.0], [–1.0, 1.0]]) # define the total iterations n_iter = 60 # steps size alpha = 0.02 # factor for average gradient beta1 = 0.8 # factor for average squared gradient beta2 = 0.999 # perform the gradient descent search with adam best, score = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) |
Tying all of this together, the complete example of gradient descent optimization with Adam is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
# gradient descent optimization with adam for a two-dimensional test function from math import sqrt from numpy import asarray from numpy.random import rand from numpy.random import seed
# objective function def objective(x, y): return x**2.0 + y**2.0
# derivative of objective function def derivative(x, y): return asarray([x * 2.0, y * 2.0])
# gradient descent algorithm with adam def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e–8): # generate an initial point x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0]) score = objective(x[0], x[1]) # initialize first and second moments m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # run the gradient descent updates for t in range(n_iter): # calculate gradient g(t) g = derivative(x[0], x[1]) # build a solution one variable at a time for i in range(x.shape[0]): # m(t) = beta1 * m(t-1) + (1 – beta1) * g(t) m[i] = beta1 * m[i] + (1.0 – beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 – beta2) * g[i]**2 # mhat(t) = m(t) / (1 – beta1(t)) mhat = m[i] / (1.0 – beta1**(t+1)) # vhat(t) = v(t) / (1 – beta2(t)) vhat = v[i] / (1.0 – beta2**(t+1)) # x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + eps x[i] = x[i] – alpha * mhat / (sqrt(vhat) + eps) # evaluate candidate point score = objective(x[0], x[1]) # report progress print(‘>%d f(%s) = %.5f’ % (t, x, score)) return [x, score]
# seed the pseudo random number generator seed(1) # define range for input bounds = asarray([[–1.0, 1.0], [–1.0, 1.0]]) # define the total iterations n_iter = 60 # steps size alpha = 0.02 # factor for average gradient beta1 = 0.8 # factor for average squared gradient beta2 = 0.999 # perform the gradient descent search with adam best, score = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) |
Running the example applies the Adam optimization algorithm to our test problem and reports the performance of the search for each iteration of the algorithm.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that a near-optimal solution was found after perhaps 53 iterations of the search, with input values near 0.0 and 0.0, evaluating to 0.0.
|
… >50 f([-0.00056912 -0.00321961]) = 0.00001 >51 f([-0.00052452 -0.00286514]) = 0.00001 >52 f([-0.00043908 -0.00251304]) = 0.00001 >53 f([-0.0003283 -0.00217044]) = 0.00000 >54 f([-0.00020731 -0.00184302]) = 0.00000 >55 f([-8.95352320e-05 -1.53514076e-03]) = 0.00000 >56 f([ 1.43050285e-05 -1.25002847e-03]) = 0.00000 >57 f([ 9.67123406e-05 -9.89850279e-04]) = 0.00000 >58 f([ 0.00015359 -0.00075587]) = 0.00000 >59 f([ 0.00018407 -0.00054858]) = 0.00000 Done! f([ 0.00018407 -0.00054858]) = 0.000000 |
Visualization of Adam
We can plot the progress of the Adam search on a contour plot of the domain.
This can provide an intuition for the progress of the search over the iterations of the algorithm.
We must update the adam() function to maintain a list of all solutions found during the search, then return this list at the end of the search.
The updated version of the function with these changes is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# gradient descent algorithm with adam def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e–8): solutions = list() # generate an initial point x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0]) score = objective(x[0], x[1]) # initialize first and second moments m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # run the gradient descent updates for t in range(n_iter): # calculate gradient g(t) g = derivative(x[0], x[1]) # build a solution one variable at a time for i in range(bounds.shape[0]): # m(t) = beta1 * m(t-1) + (1 – beta1) * g(t) m[i] = beta1 * m[i] + (1.0 – beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 – beta2) * g[i]**2 # mhat(t) = m(t) / (1 – beta1(t)) mhat = m[i] / (1.0 – beta1**(t+1)) # vhat(t) = v(t) / (1 – beta2(t)) vhat = v[i] / (1.0 – beta2**(t+1)) # x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + ep x[i] = x[i] – alpha * mhat / (sqrt(vhat) + eps) # evaluate candidate point score = objective(x[0], x[1]) # keep track of solutions solutions.append(x.copy()) # report progress print(‘>%d f(%s) = %.5f’ % (t, x, score)) return solutions |
We can then execute the search as before, and this time retrieve the list of solutions instead of the best final solution.
|
... # seed the pseudo random number generator seed(1) # define range for input bounds = asarray([[–1.0, 1.0], [–1.0, 1.0]]) # define the total iterations n_iter = 60 # steps size alpha = 0.02 # factor for average gradient beta1 = 0.8 # factor for average squared gradient beta2 = 0.999 # perform the gradient descent search with adam solutions = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) |
We can then create a contour plot of the objective function, as before.
|
... # sample input range uniformly at 0.1 increments xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(x, y, results, levels=50, cmap=‘jet’) |
Finally, we can plot each solution found during the search as a white dot connected by a line.
|
... # plot the sample as black circles solutions = asarray(solutions) pyplot.plot(solutions[:, 0], solutions[:, 1], ‘.-‘, color=‘w’) |
Tying this all together, the complete example of performing the Adam optimization on the test problem and plotting the results on a contour plot is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
# example of plotting the adam search on a contour plot of the test function from math import sqrt from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D
# objective function def objective(x, y): return x**2.0 + y**2.0
# derivative of objective function def derivative(x, y): return asarray([x * 2.0, y * 2.0])
# gradient descent algorithm with adam def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e–8): solutions = list() # generate an initial point x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0]) score = objective(x[0], x[1]) # initialize first and second moments m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # run the gradient descent updates for t in range(n_iter): # calculate gradient g(t) g = derivative(x[0], x[1]) # build a solution one variable at a time for i in range(bounds.shape[0]): # m(t) = beta1 * m(t-1) + (1 – beta1) * g(t) m[i] = beta1 * m[i] + (1.0 – beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 – beta2) * g[i]**2 # mhat(t) = m(t) / (1 – beta1(t)) mhat = m[i] / (1.0 – beta1**(t+1)) # vhat(t) = v(t) / (1 – beta2(t)) vhat = v[i] / (1.0 – beta2**(t+1)) # x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + ep x[i] = x[i] – alpha * mhat / (sqrt(vhat) + eps) # evaluate candidate point score = objective(x[0], x[1]) # keep track of solutions solutions.append(x.copy()) # report progress print(‘>%d f(%s) = %.5f’ % (t, x, score)) return solutions
# seed the pseudo random number generator seed(1) # define range for input bounds = asarray([[–1.0, 1.0], [–1.0, 1.0]]) # define the total iterations n_iter = 60 # steps size alpha = 0.02 # factor for average gradient beta1 = 0.8 # factor for average squared gradient beta2 = 0.999 # perform the gradient descent search with adam solutions = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) # sample input range uniformly at 0.1 increments xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(x, y, results, levels=50, cmap=‘jet’) # plot the sample as black circles solutions = asarray(solutions) pyplot.plot(solutions[:, 0], solutions[:, 1], ‘.-‘, color=‘w’) # show the plot pyplot.show() |
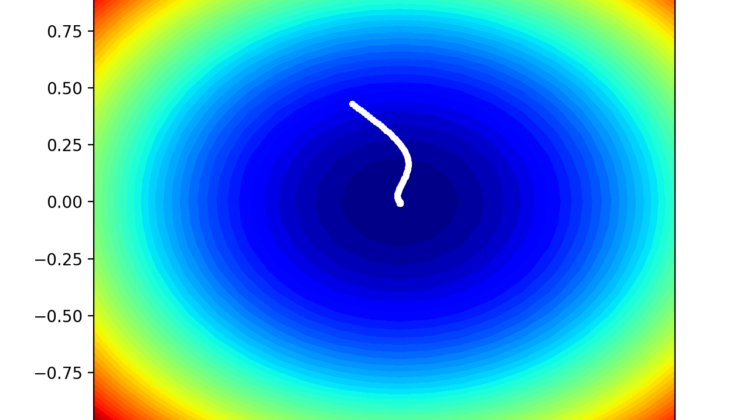
Running the example performs the search as before, except in this case, a contour plot of the objective function is created.
In this case, we can see that a white dot is shown for each solution found during the search, starting above the optima and progressively getting closer to the optima at the center of the plot.
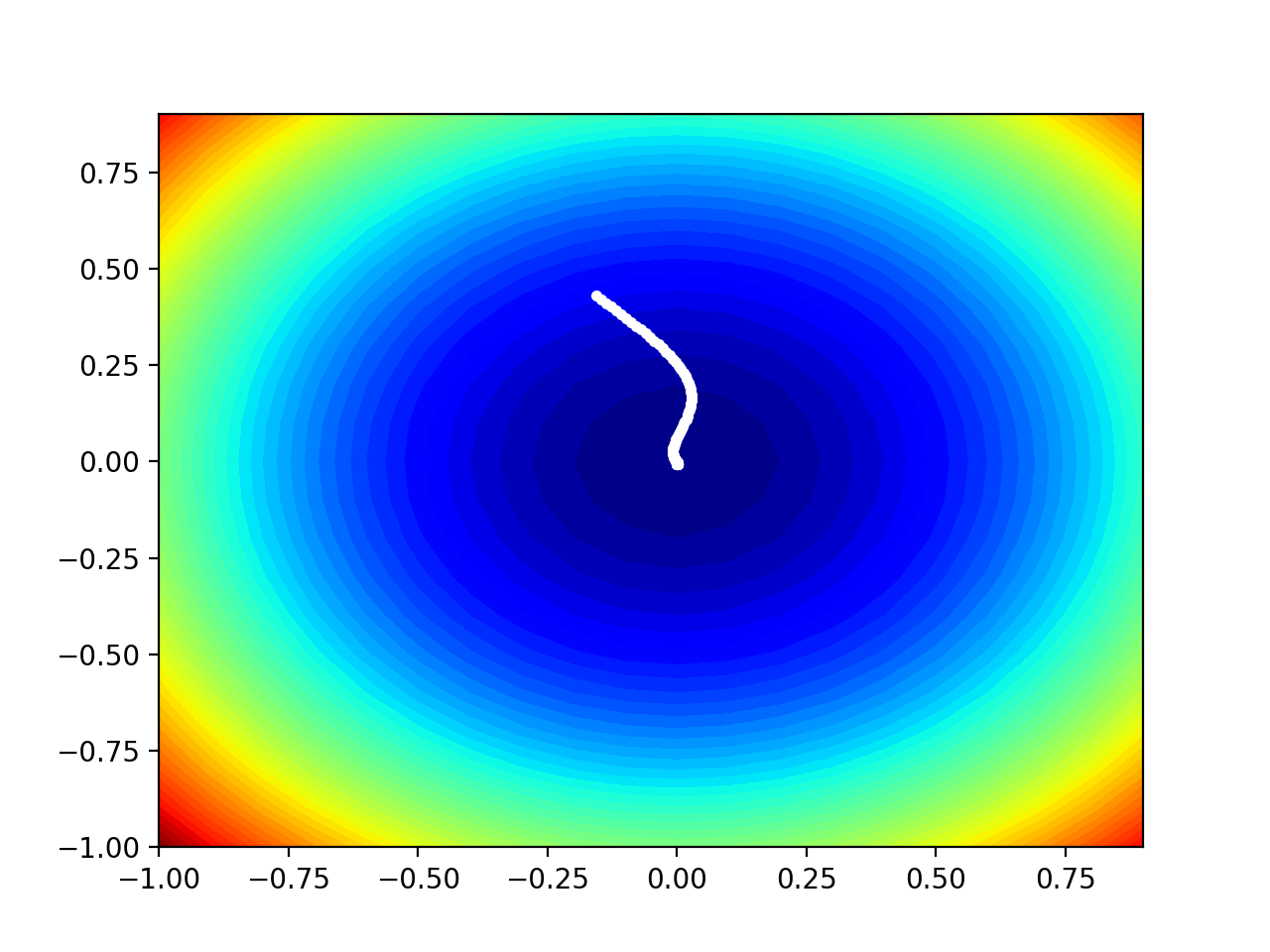
Contour Plot of the Test Objective Function With Adam Search Results Shown
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
Books
APIs
Articles
Summary
In this tutorial, you discovered how to develop gradient descent with Adam optimization algorithm from scratch.
Specifically, you learned:
- Gradient descent is an optimization algorithm that uses the gradient of the objective function to navigate the search space.
- Gradient descent can be updated to use an automatically adaptive step size for each input variable using a decaying average of partial derivatives, called Adam.
- How to implement the Adam optimization algorithm from scratch and apply it to an objective function and evaluate the results.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
