In this article, we will study some important data preprocessing methods. It is a very important step to visualize the data and make it in a suitable form so that the estimators (algorithm) fit well with good accuracy.
Topics to be covered:
- Standardization
- Scaling with sparse data and outliers
- Normalization
- Categorical Encoding
- Imputation
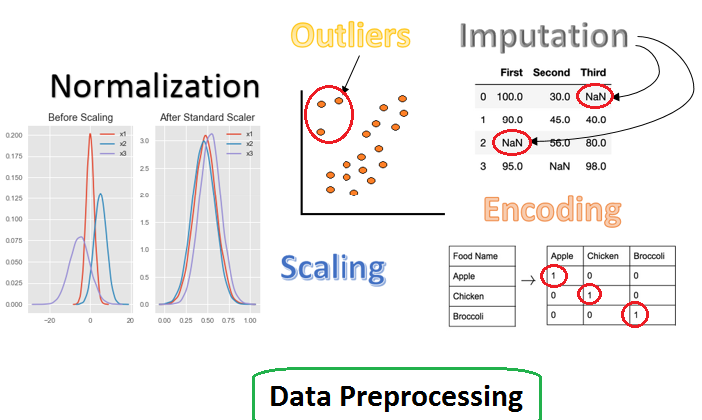
Standardization
Standardization is a process that deals with the mean and standard deviation of the data points. As raw data, the values are varying from very low to very high. So, to avoid the low performance in the model we use standardization. It says, the mean becomes zero and the standard deviation becomes a unit.
The formula to standardization shown below:
z = (feature_value — mean)/standard deviation
When we use an algorithm to fit our data it assumes that the data is centered and the order of variance of all features are the same otherwise the estimators will not predict correctly.
The sklearn library has a method to standardize the data set with StandardScaler in preprocessing class.
We use the import command to use this feature in python.
#Before modeling our estimator we should always some preprocessing scaling.# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Scaling with sparse data and outliers
Scaling with Sparse data:
Scaling of data is another way of making feature values be in some range of “0” and “1”. There are two methods of doing these i.e. MinMaxScaler and MaxAbsScaler.
Example with python
import numpy as np
X_train = np.array([[ 1., 0., 2.], [ 2., 0., -1.], [ 0., 2.,
-1.]])from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler()X_train_minmax = min_max_scaler.fit_transform(X_train)print(X_train_minmax)#output:
array([[0.5, 0. , 1. ],
[1. , 0. , 0. ],
[0. , 1. , 0. ]])
As we see the input value comes in a range of “0” and “1”.
Creating scaling of the sparse data centering is not a good idea because it may change its structure. So, it is good to scale the input raw data that has values on different scales.
Scaling with Outliers:
When raw data have many outliers then the scaling with mean and variance doesn’t do well with the data. So, we have to use a more robust method like the interquartile method (IQR) because the outliers are influenced by mean and variance. The range of the IQR is between 25% and 75% in which the median is removed and scaling the quantile range.
The RobustScaler takes some parameters to perform scaling.
- The first parameter is
with_centeringthat centers the data before scaling if it is true. - The second parameter is
with_scalingif it is true then it scale the data in the quantile range.
Example with python
from sklearn.preprocessing import RobustScaler
X = [[ 1., 0., 2.], [ 2., 0., -1.], [ 0., 2., -1.]]
transformer = RobustScaler().fit(X)transformer.transform(X)#output:
array([[ 0., 0., 2.],
[ 1., 0., 0.],
[-1., 2., 0.]])
Normalization
The scaling process in this is to normalize the values to their unit norm. An example of this normalization is MinMaxScaler. The process is useful when we are dealing with quadratic form in pair forms it can be kernel-based or dot product-based.
It is also useful based on of vector space model i.e the vectors related with text data samples to ease in data filtration.
Two types of Normalization happen as shown below:
- Normalize: It deals to scale the input vectors to unit norm. The norm parameter is used to normalize all the non-zero values. It takes three arguments L1, L2, and max where the L2 is the default norm.
- Normalizer: It also does the same operation but in this process the fit method is optional.
Example with Python:
from sklearn.preprocessing import normalize
X = [[ 1., 0., 2.], [ 2., 0., -1.], [ 0., 2., -1.]]
X_normalized = normalize(X, norm=’l2')print(X_normalized)#output:
array([[ 0.4472136 , 0. , 0.89442719],
[ 0.89442719, 0. , -0.4472136 ],
[ 0. , 0.89442719, -0.4472136 ]])
Example with Normalizer:
from sklearn.preprocessing import Normalizer
X = [[ 1., 0., 2.], [ 2., 0., -1.], [ 0., 2., -1.]]normalizer = preprocessing.Normalizer().fit(X)normalizer.transform(X)#output:
array([[ 0.4472136 , 0. , 0.89442719],
[ 0.89442719, 0. , -0.4472136 ],
[ 0. , 0.89442719, -0.4472136 ]])
The normalizer is useful in the pipeline of data processing in the beginning.
When we use sparse input it is important to convert it not CSR format to avoid multiple memory copies. The CSR is compressed Sparse Rows comes in scipy.sparse.csr_matrix.
Categorical Encoding
When we get some raw data set then some columns are that are not in continuous values rather in some categories of binary and multiple categories. So, to make them in integer value we use encoding methods. There are some encoding methods given below:
- Get Dummies: It is used to get a new feature column with 0 and 1 encoding the categories with the help of the pandas’ library.
- Label Encoder: It is used to encode binary categories to numeric values in the sklearn library.
- One Hot Encoder: The sklearn library provides another feature to convert categories class to new numeric values of 0 and 1 with new feature columns.
- Hashing: It is more useful than one-hot encoding in the case of high dimensions. It is used when there is high cardinality in the feature.
There are many other encoding methods like mean encoding, Helmert encoding, ordinal encoding, probability ratio encoding and, etc.
Example with Python:
df1=pd.get_dummies(df['State'],drop_first=True)
Imputation
when raw data have some missing values so to make the missing record to a numeric value is know as imputing.
Creating the random data frame.
# import the pandas library
import pandas as pd
import numpy as npdf = pd.DataFrame(np.random.randn(4, 3), index=['a', 'c', 'e',
'h'],columns=['First', 'Second', 'Three'])df = df.reindex(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'])print (df)
Now replacing with zero value.
print ("NaN replaced with '0':")
print (df.fillna(0))
Replacing the missing values with mean.
from sklearn.impute import SimpleImputer
imp = SimpleImputer(missing_values=np.nan, strategy='mean')
The sklearn provide simple imputer to find the NAN values and fill with mean.
We can use imputer in the pipeline to make an estimator better.
Conclusion:
The data preprocessing is an important step to perform to make the data set more reliable to our estimators.
I hope you like the article. Reach me on my LinkedIn and twitter.
2. Python Data Structures Data-types and Objects
3. Python: Zero to Hero with Examples
4. Fully Explained SVM Classification with Python
5. Fully Explained K-means Clustering with Python
6. Fully Explained Linear Regression with Python
7. Fully Explained Logistic Regression with Python
8. Basics of Time Series with Python
