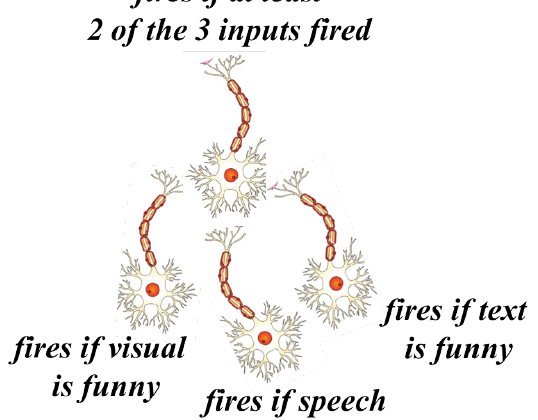
Neural Networks are a condensed, ripped-off version of the way our brain functions. Our nervous system is made up of millions of neurons connected to each other sequentially. The brain makes decisions based on which neurons fire and by how much. For example, when you’re watching The Office and come across a joke, what do you think happens in that skull of yours?
- There is a massively parallel interconnected network of neurons.
- The sense organs relay information (input) to the lowest layer of neurons.
- Some of these neurons may fire and may relay the information to the next few layers of neurons.
- Each neuron performs a certain role or responds to a certain stimulus.
- This massively parallel network also ensures division of labour.
- This process continues till the topmost layer of neurons in the brain, which will fire only when the firing neurons in the penultimate layer are more than a certain threshold level (here, it’s 2 out of 3 neurons).
It’s as simple as that.
Your neural network extracts meaningful information from the given inputs, relays it on to make draw further insights and features and provides the result as the output.
Artificial neural networks work with the exact same principle. Deep Learning focusses on using input data to figure out patterns within them, or determine mathematical relations between the inputs and the outputs which can be used to further extrapolate and predict trends based on previous inputs.
What we saw just now is an overly simplified version of how the brain works, but it suffices for our discussion on Neural Nets. Before understanding how a complete network functions, it’s essential to look at how individual neurons work and how they can be modified to suit different needs.
In 1943, the simplest computational model of a neuron (McCulloch-Pitts Neuron) was introduced.
‘g’ aggregates the inputs and ‘f’ takes a decision based on this aggregation.
The inputs can be excitatory (1) or inhibitory (0).
In the traditional model, y = 0 if the sum of all inputs is lesser than a given threshold.
‘Theta’ here is the threshold parameter.
Based on the above criteria, we can replicate boolean functions using a single neuron:
*circle at the end indicates inhibitory input: if any inhibitory input is 1 then output will be 0.
As you probably noticed, McCulloch-Pitts Neuron doesn’t come without its own set of limitations.
- What about non-boolean (real valued) functions?
- Do we need to set the threshold by hand?
- What if we want to assign more importance to some inputs?
To counter these short-comings, the perceptron was introduced in 1958. The main differences are:
- Inputs are no longer restricted to boolean values
- Numerical weights introduced for each input
- There exists a mechanism (algorithm) to learn these weights automatically
‘Theta’ is the threshold, ‘w’ are the weights while ‘x’ are individual inputs.
Hence, a perceptron can assign more weightage to certain inputs and take decisions based on how the collective sum fares against the threshold value.
However, the threshold logic of a perceptron is a bit too harsh.
Consider an example: you’re building a single-neuron system which will decide if a movie is worth going to. You set the threshold to a rating of 0.5 out of 1.
The output function for a perceptron.
According to this system, the switch from “no, this movie is trash” to “yes, this movie deserves an Oscar” is rather too immediate.
Moreover, this system would return y = 0 (do not watch) if the ratings were 0.49, which is rather strange as it is close to 0.5 (which happens to be my threshold).
What we need, is a system response that has a smoother decision function.
This calls for a change in the function employed by neurons. Introducing a sigmoid neuron can help with a gradual function suitable for real-world applications.
Blue: Perceptron output vs Red: Sigmoid output.
Sigmoid function is a family of functions, some of which are:
- tanh function
- Logistic function
- Softmax function
Furthermore, the output is not binary, but is a real-valued decimal which can be interpreted as probability.
An example of the sigmoid function is the logistic function (in graph):
Sigmoid functions are also smooth, continuous and differentiable at all points.
Neurons are used to derive insights into certain patterns posed by input data to obtain mathematical functions that best fit the input data points with minimal error.
A McCulloch-Pitts neuron can generate a linear function in n-dimensions (a line, or a plane or a hyperplane). It only holds good for linearly separable functions (functions which return y = 1 above the line/plane and return y = 0 below the line/plane).
However, it is not possible to generate a non-linear function which can accurately classify the red points and blue points separately (in the adjacent figures) using a single neuron.
To generate non-linear functions that can approximately traverse between points to classify most of them accurately, you’ll have to use a network of neurons interconnected layer-wise. Each layer finds different patterns and transmits forward, where they become more profound.
You can try working on different functions in the Neural Network Playground from TensorFlow. Its fun, its foolproof, and you don’t need to be a nerd to be able to use it.
So based on individual neuron behaviour, we present a fully working artificial feed-forward neural network!
An artificial neural network. Notice how each input is connected to every neuron.
Terminology:
- This network contains 3 layers.
- The layer containing the inputs is called the input layer.
- The middle layer containing the 4 perceptrons is called the hidden layer.
- The final layer containing the output neuron is called the output layer.
- The outputs of the 4 perceptrons in the hidden layer are denoted by h1, h2, h3 and h4.
- The red and blue edges are called layer 1 weights.
- w1, w2, w3 and w4 are called layer 2 weights.
In order to enable the neural network replicate the desired function with minimal error, we need to employ some techniques which will ensure that the standard output function (sigmoid function/ perceptron output summation) is moving towards the function we’re looking for. One way to gauge the accuracy of the output with respect to the function is by using a loss function.
Loss functions are metrics that help in keeping track of how distant the outputs of the neural network are from the desired function values. One example of loss functions is the famous squared error loss:
‘y-hat’ is the output of the neural network. ‘y’ is the expected output from the desired function.
We know, from a single neuron we have:
‘w’ stands for the weights employed in the network. Remember, it is a matrix whose elements are individual weights. ‘x’ is a vector containing the inputs.
With a combination of these neurons, we will end up getting an arbitrary output in the first iteration, i.e. when we provide inputs and random weights in the beginning. We need the neural network to learn how the weights ‘w’ can be altered in order to bring the output function (y-hat) as close to the desired function as possible. (The closeness to the desired function is determined by the value of the loss function).
So we’ve got ourselves an optimization problem: minimize the loss function.
In order to minimize the loss function, we employ a matrix calculus based optimization technique called Gradient Descent.
You’ve previously seen that the neurons accumulate the inputs in the form (Wx + b) where ‘W’ and ‘b’ are the corresponding weight and bias respectively. Gradient Descent is a method to determine the required weights and biases by moving along the path opposite to the gradient so as to reach the global minima of the error surface.
Gradient Descent observed graphically. Notice how the error decreases along the steepest slope only.
Hold up. Catch a breather. Here’s everything you read about a network of neurons till now, ultra condensed:
- You need to achieve a certain function exhibited by the points in your dataset.
- You have functions such as the sigmoid and perceptron sum in your inventory. Your network of neurons need to find which parameters in your sigmoid function can be tweaked, and by how much, in order to bring your function as close to the desired one as possible.
- Your function will be deemed closely accurate to the desired function if the loss function is minimal (ideal cases, zero).
- Random weights are fed to the neural network along with the input.
- The output is obtained for different values of x (different inputs). Of course, the output is arbitrary and is nowhere close to the function you want. Consequently, the loss function value is high.
- Here’s where things get interesting and confusing (mainly because you’re going to hear names of topics that’re covered below, but don’t bother for now). Your neural network performs backpropagation (where all the gradients are computed) and subsequently performs gradient descent to ensure that new weights are assigned in a manner which decreases the loss function.
- The network repeats the above step repeatedly till the loss reaches the global minima.
Well done, you’re much more confused than you were before. But stick around, and you’ll find out what backpropagation and gradient descent actually do. Then you can come back here and summarize the whole thing for yourself 😉
For example, in a simple neural network with perceptrons, we know:
Therefore, for a 2-layered neural network, we can write the output expressions as:
Thus, in Gradient Descent, we aim to make changes to the ‘W’ matrix and the ‘b’ vector in order to bring our output function as close to the desired function as possible, iteration-wise, slowly.
Thus, under Gradient Descent in each iteration, ‘w’ and ‘b’ are changed as follows:
Of course, the above step is performed iteratively to compute gradients, tweak ‘w’ and ‘b’, find the outputs for each neuron and compare them against the desired function using the loss function metric. The whole task is computationally intensive and requires quite a robust PC configuration, especially when you’re working with many layers, or images (they use specific preprocessing techniques like convolution and pooling before actually being fed into the neural network, so we’ll take those up in the coming weeks).
Check out what the code looks like. You’ll understand the algorithm better.
Thus, in a feedforward neural network we’ve observed that a function can be closely replicated by helping it learn how to minimize the error. Also, each neuron has a pre-activation and an activation part.
Pre-activation is basically the weighted sum of all inputs, and is represented as ‘a’.
Activation function is what converts the weighted sum into a point on the curve of the desired function. For example, a sigmoid neuron with the logistic function as the activation function will perform as:
We’ll represent the activation function output f(x) as ‘h’ here on.
Some commonly used activation functions are the softmax, linear, tanh, relu, etc. They’re relatively easier to grasp (after all, they’re just mathematical formulae) and you can read up on effect of activation online.
Here’s a figure to help you understand the activation jargon better.
