Artificial intelligence as the name suggests means providing intelligence to computers, similar to what humans possess. Consider AI as a big umbrella consisting of ANI (Artificial Narrow Intelligence) — goal-oriented and programmed for a single task, AGI (Artificial General Intelligence) — allowing the machine to behave in a manner that they are indistinguishable from humans and ASI (Artificial Super Intelligence) — machine behaving smarter than the brightest human minds.
Machine Learning is a subset of AI where, given the data and the algorithm, the machine automatically trains itself and gets smarter without human intervention. There are 3 types of ML algorithms — supervised, unsupervised and reinforcement.
Deep Learning emulates how a human brain functions (hence it has neurons, networks, etc. similar to what the human brain has). When the amount of data starts increasing, ML can only cope up to a certain point after which it saturates. This is where Deep Learning comes into play — DL is a type of ML which is used over a large dataset.
The idea of how perceptron works, the building block of deep learning, was discovered back in 1958 so why was DL not used then, and is being used now extensively? DATA! Running an ML algorithm takes up much fewer resources as compared to running a DL algorithm and with the amount of data available with us back in 1958, we were doing just fine with ML. But with the advancements in hardware (GPUs etc.), software (New models, toolboxes etc.) and an increase in the amount of data — we are at a stage that we NEED to use DL in order to increase the model’s performance
In order to understand how DL algorithms work, we first need to understand how a Perceptron works. For simplicity, you can consider that majority of the DL models are just mixing up multiple perceptions, that’s it. It’s like if you understand what numbers mean (i.e.perceptron), then it’s easy for you to do addition and subtraction(i.e.DL models) with them.
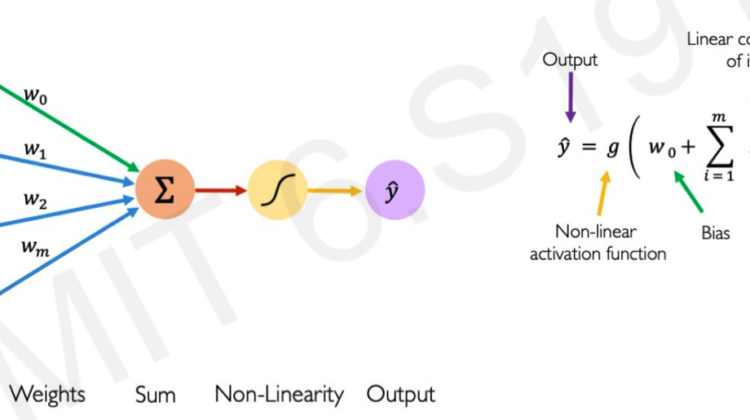
A perceptron is a neural network unit that does certain computations to detect features or business intelligence in the input data.
Intuition: Consider you want to buy a house — you will take into consideration multiple factors like location(x1), # of bedrooms(x2), total area(x3), pet-friendly (x4), distance from work(x4) etc. There are some factors which are more important to you than others, for e.g. location and # of bedrooms, so you would give different importance to each of them when making a decision. So when your brain wants to make an intermediate-decision, it will take the factors along with the importance into consideration and add a little bias that it has developed over the years (for e.g. if you have been eating white bread all day, your brain will have a bias for selecting white bread over brown bread). This is exactly how a perceptron operates.
In the diagram above, the factors you took into consideration are the inputs, the importance you provided to each factor are the weights and the intermediate-decision you took is just a linear combination of the inputs and the bias(orange node).
The only difference between your brain and a DL perceptron is that you need to apply a NON-LINEAR makeup (in DL it’s called activation function) to convert your intermediate-decision to a final decision. Why non-linear and not linear? Look at the below diagram
There are different non-linear functions that you can apply to your intermediate-decision — sigmoid, ReLU, Hyperbolic etc., we will get to that later.
To summarize, we can say that the final decision(y) in Fig 1.1 is just the non-linear makeup(g) applied to your intermediate-decision(z) — this is how a perceptron works aka forward propagation
Don’t you think that instead of having just one intermediate-decision(z) to come up with a final one(y), it will be easier to have multiple intermediate-decisions(z1,z2,z3,…) helping you make the final call(y)? We just described a single neural network. The collection of multiple intermediate-decisions is what is called a ‘hidden layer’ in the DL jargon
In the above example, they have used the hidden layer to spit out two decisions (y1 and y2), you can have one decision as well.
Applying Neural Networks:
Intuition: Let’s take a simple example of tuning a guitar. Let’s say you want to tune the E chord — you pluck the string and check if it’s matching with the E chord. If you feel that the difference in what your E chord is sounding and what it is supposed to sound like is big then you tighten or loosen the knob to get the string closer to sounding like an E chord. After a few tries of tightening and loosening the knob, you find the perfect balance to hit the E chord — that is how your brain works and that is exactly how neural network works.
In the case of neural networks, consider the action of plucking the string as input, the knob as weights. So we start the neural network by
- Step 1: Giving inputs (plucking the string) and calculating the empirical loss (understand the difference between what it is supposed to sound like and what it is sounding like),
- Step 2: Based on the loss, we adjust our weights (knobs).
This process is also called backpropagation
Step 1: Calculating Empirical loss
This is how the empirical loss is calculated:
So if you see, it’s primarily the difference in what your model gives and what it is supposed to give. As we know that there are different types of output that we can expect: binary (0/1) or continuous real numbers, there are different ways to calculate losses for each of them (see below)
Cross entropy loss for binary output:
Mean squared error for continuous numbers output:
Step 2: Optimizing our loss
Now that we have our loss, as mentioned, we will need to adjust our weights (knobs) to bring down the loss — this process is called “Loss Optimization”.
In order to lower the loss, we use the “Gradient Descent” algorithm.
It is very simple:
- You first start with understanding where currently you are.
- You then take the derivative of the loss function aka calculating the gradient — you would ask why take the DERIVATIVE? Taking derivative gives you the direction in which you should go if you want to maximize your loss. Wait! but don’t we need to minimize our loss? Definitely, hence in the formulae below, you will observe that we have a negative sign in front of the derivative.
- You start taking small steps towards the direction by adjusting weights using the gradient — how small the steps are, is defined by the “learning rate” (see Step 4 of Fig 2.6)
Loss functions are difficult to optimize because it’s difficult to know how small do we need to take the steps (learning rate). If it’s too small, you will might get stuck in local minima, and if it’s too big, you will keep bouncing off and never reach global minima.
There are variants of gradient descent that help you with this:
- Stochastic Gradient Descent
- Adam
- Adadelta
- Adagrad
- RMSProp
Intuition: Let’s say you have an exam coming up and you have been given a question bank to revise your material. Instead of revising, you use the Q Bank as the only source of studies and try to learn only the questions from the bank. So when you appear for the exam, you might know answers to questions that were in Q Bank but won’t be able to answer questions that are out of the Q bank but somewhat related to those. This is overfitting.
To solve this, we have what is called “Regularization” — this helps in increasing the generalization of our model on unseen data, in our case questions that are not on Q Bank. Different types of regularization techniques are:
- Dropout — during training, randomly set some activations to 0
- Early stopping — stop training as soon as the loss on the testing set starts increasing. Note: loss on training set will never increase (see Fig 2.8)
- Allocate random weights
- Get the initial predictions
- Compute the loss
- Try optimizing the loss: using SGD, Adam, Adaboost
- Avoid overfitting: Regularization- Dropout, Early stopping
