Gradient Descent Intuition
It is an algorithm that updates a machine learning model’s parameters to reduce the error (the difference between the actual and predicted values). After forward propagation, we calculate the loss function to know how a model is doing to predict the target values. For example, mean squared error is a popular loss function. Then the gradient descent or optimizer updates the weight parameters by calculating derivatives of the cost function with respect to weight parameters ( often represented as W) to predict more accurately. Gradually the error is reduced by this process.
So gradient descent takes the derivative(slope) of the cost function with respect to W to find out how to update the parameter W (i.e. should the values of W be increased or decreased ? ) so that the cost function is minimized.
For example:
Let, the weight parameters be W. Then the update rule for the weight parameter W will be:
Here alpha is the learning rate that defines step size. If alpha has a bigger value then after each calculation of the derivatives the weight parameter will take a big step (the difference between the previous value and the new updated value of the W would be big) for its increase or decrease. If alpha is small then the change would be small. W contains all the learning parameters from 0 to n (if we have n parameters for learning; this is represented as a matrix).
Now, for understanding how each step works in a gradient descent I will try to explain it with some pictures!
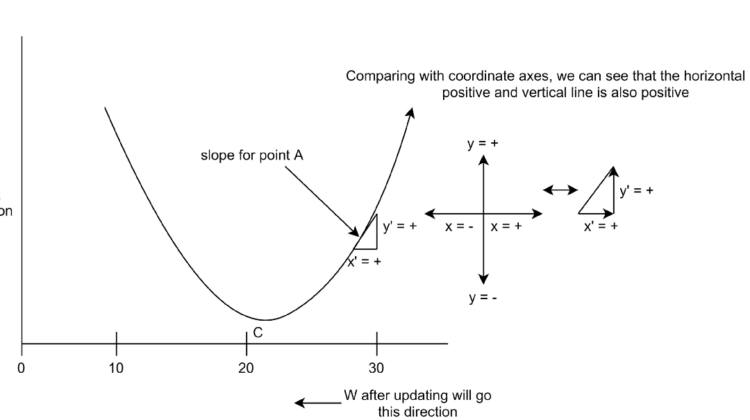
PICTURE 1:
In picture 1, the curved line in the 2d space is the cost function and the lowest point C is our goal to reach after running our gradient descent algorithm several times to make our cost function minimized. Suppose at some point the W value is in the A point of the cost function. Now to go in the direction of the lowest point our gradient descent algorithm will work as the defined equation in 1. If we take derivatives at the A point we will have a positive slope (as shown in pic 1). This positive value will then be multiplied with alpha.
So as we subtract the positive value by finding the slope from the W matrix, W values will go in the left direction (W value will become smaller). So the values in W will be changed in such a way that it will approach the lowest point C in which point our cost function will be minimized and our algorithm or model will predict in an optimized way.
PICTURE 2:
In Picture 2, consider W or parameter value is in point B. So if we take the slope in the B point it will be negative (as shown in picture 2). Now if we look into equation 1 we can see that we have a default minus sign. Now as we got our slope negative, the value of the derivative will become positive when we put the value in equation 1.
So the W value will be updated accordingly (W value will become bigger)and it will be directed towards the lowest point C.
That is how gradient descent works and optimizes the cost function and updates the W values (weights) of a network for making more accurate predictions. Hope the picture and explanation help :).
