Recent years have witnessed the effectiveness of machine learning (ML) in solving computer systems optimization problems by modeling resources’ complicated, non-linear interactions. The standard way to incorporate ML into a computer system is to first train a learner to accurately predict the system’s behavior as a function of resource usage — e.g., to predict energy efficiency as a function of CPU usage — and then deploy the learned model as part of a system — e.g., a scheduler. Much prior work has applied existing ML directly and believed that the increased prediction accuracy would guarantee a better system outcome. However, is this the real case?
The answer is NO! In this post, I will show that higher prediction accuracy is NOT equivalent to a better system outcome through a real example. The data is from our ISCA 2019 paper.
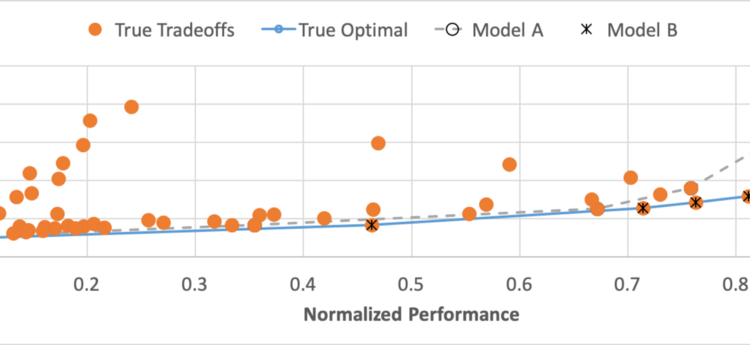
We run a real application SRAD on an ARM big.LITTLE system. Figure 1 shows the normalized performance (x-axis) and power (y-axis) tradeoffs. Each point is a configuration (combination of core allocation and clockspeed) and its position represents its performance and power tradeoffs. The dots are all possible configurations, while the solid line is the frontier of true optimal tradeoffs (found through exhaustive search). A key intuition is: for any application, most points do not represent optimal tradeoffs. In this example, only 10 of 128 configurations are on the optimal frontier.
We also construct two learned models: A and B. Both models predict the application’s true power and performance tradeoffs as a function of the system configurations.
Model A uses the true, measured data for the non-optimal points and then deliberately moves the optimal points just far enough that they will not be selected by the scheduler. Model A’s accuracy in goodness-of-it is 99%. We measure energy by feeding this model to a scheduler and having it select configurations to meet latency requirements and minimize energy. We vary latency requirements across the range of possible behaviors and ensure they are met at least 99% of the time. We then measure the energy and compare to optimal — i.e., that obtained with a perfect model. We find that Model A uses 22% more energy than optimal.
In contrast, Model B uses the true data for the optimal configurations, all others are assigned minimal performance and maximum power. Model
B’s goodness-of-fit is essentially 0 — not surprising, as most points are inaccurately predicted. All the optimal points are predicted with no error, however, so the energy is the same as optimal.
To summarize, Model A gets near perfect accuracy, but high energy; Model B has poor accuracy, but optimal energy.
- High accuracy does not necessarily imply a good systems result.
- Low accuracy does not necessarily mean a bad systems result.
- The system disproportionately benefits from improving accuracy of the small set of configurations on the optimal frontier, which is called asymmetric benefits.
- Learning for systems optimization may have reached a point of diminishing returns where accuracy improvements have little effect on the systems outcome.
- We advocate that future work should de-emphasize accuracy and instead incorporate the system problem’s structure into the learner. Our paper also shows how to incorporate structure to the learner to improve the system outcome.
