Machine Learning problems always deals with the datasets itself . Real world Data are need some feature Engineering techniques which may contain null values and categorical variables as well. This can arises due to human error or it can be from sensor itself. But we can also obtained such readymade datasets from Kaggle itself such as housing price prediction, sales prediction. For the brief intro, Readymade datasets are those which have no null values, need no type of feature selection techniques. The behaviour of each point in a dataset can be visualized by matplotlib pyplot function. Its important to visualize our datasets before approaching any machine learning task.
As per visualization, there are several algorithms discussed for regression model upon which model fits the best. The most common regression problem for any prediction is Linear Regression, Lasso Regression, Ridge Regression. They are applied depending upon the behaviour and the nature of datasets . Suppose someone wants to predict a prices of the house depending on the attributes that house possesses. It’s quite easy to fit regressional model on such scenerios.
There are several hyperparameters that often effects the performance of the model in the dataset and speeds up its accuracy level. Selecting a hyperparamter for a model that fits the best is quite often a tedious work. To avoid such type of complexities, the algorithms like GridSearchCV or RandomizedSearchCV have been introduced. Both works fine inspite of having few drawbacks.
As per the introduction, lets focus firstly on Linear Regression which is the one of the common application for continuous data such as housing price predictions. In Linear Regression, Line Curve is almost straight forward which is the best fitted option for the linear based datasets. Line Curve is the continuous line that have finite curvature. Line Curve can also be complex depending upon the datapoints on the datasheet. In almost all real life situations, line curve have non zero curvature(i.e. curved line)with best suited hyperparameters that fits well
Focusing on a fact that model performs well on a linearly spaced datasets, Line Curve follow the straight line equation (y = mx + c) where m is the slope of the straight line and c is the intercept. Datasets comprises input, features and the target variables. More you collected data samples, better will be your the model performance and its accuracy. The model trained on many features should be given importances according to its weights.
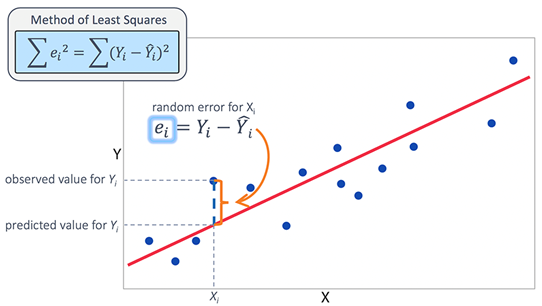
where h0, h1, h2,…. are the weights given to the features for predictions to a model to compute its accuracy. Below is a diagram illustrating Linear Regression graph which shows a linear correlation between features and the target variable.
Best Fit Line is chosen such that average mean squared error between the actual and predicted value is much less as possible. Its not always necessary to start the fitted line from the origin itself. The summation of the difference between the actual output and the predicted output is known as Least Squared Error. Mean Squared Error is the mean or the average over all the error in the datasets
Note: Before fitting a model into a particular datasets , we must have to perform some necessary steps in order to compute its accuracy score such as splitting of datasets, labelling the features and the target variables that will be discussed in details as we proceed furthur
Implementation :
The scikit-learn package allows you to implement a Linear Regression model by just calling a function called LinearRegression( ) . Although scikit-learn allow us to implement such algorithms much easily but there are few family members like linear_model, preprocessing, decomposition, feature_selection are introduced.
LinearRegression is present in the scikit learn’s linear_model family member and atlast we have to fit the datasets into the regression model. After the training has been completed successfully, the model is almost ready to predict on the unseen data.
There are few hyperparameters that can be used to furthur improve its model performances and speed up its process
fit_intercept : [boolean] Whether to calculate intercept for the model.
normalize : [boolean] Normalisation before regression.
copy_X : [boolean] If true, make a copy of features else overwritten.
n_jobs : [int] If -1 all CPU’s are used. This will speedup the working for large datasets to process.
To compute its accuracy, a function from sklearn.metrics to compute the r2_score . R2_score is basically “(total variance explained by model) / total variance.” So if it is 100%, the two variables are perfectly correlated, i.e., with no variance at all. Sometimes from regressor function itself, we can implement score( ) function. There are many other attributes to check its weights and c-intercept for a given best fitted line such as coef_ or intercept_ .
CONCLUSION :
This is just the basics of regression model. There are much more complexity in data that cannot be predicted by the linear regressor. For the better accuracy and performance, there are more regression algorithms to apply and their hyperparameters to make it far more better. As said earlier, real world dataset are almost messy, so some feature selection techniques must be applied to the model in order to have an effect more significantly onto the datasets.
Today I have tried my level best about how to apply a linear based regression model onto the datasets. Please follow and gets regular updates about the blogs within 24 hours and practice and learn. I am Debashis Saha trying to help my juniors with not just a roadmap but also with a regular updates of certain notes that will complete all concepts very deeply which is often not seen in regular courses.
