In a nutshell, logistic regression is multiple regression but with an outcome variable that is a categorical dichotomy and predictor variables that continuous or categorical. In pain English, this simply means that we can predict which of two categories a person is likely to belong to given certain other information.
Example: Will the Customer Leave the Network?
This example is related to the Telecom Industry. The market is saturated. So acquiring new customers is a tough job. A study for the European market shows that acquiring a new customer is five time costlier than retaining an existing customer. In such a situation, companies need to take proactive measures to maintain the existing customer base. Using logistic regression, we can predict which customer is going to leave the network. Based on the findings, company can give some lucrative offers to the customer. All these are a part of Churn Analysis.
Example: Will the Customer Leave the Network?
This example is related to the Telecom Industry. The market is saturated. So acquiring new customers is a tough job. A study for the European market shows that acquiring a new customer is five time costlier than retaining an existing customer. In such a situation, companies need to take proactive measures to maintain the existing customer base. Using logistic regression, we can predict which customer is going to leave the network. Based on the findings, company can give some lucrative offers to the customer. All these are a part of Churn Analysis.
Example: Will the Borrower Default?
Non — Performing Assets are big problems for the banks. So the banks as lenders try to assess the capacity of the borrowers to honor their commitments of interest payments and principal repayments. Using a Logistic Regression model, the managers can get an idea of a prospective customer defaulting on payment. All these are a part of Credit Scoring.
Example: Will the Lead become a Customer?
This is a key question in Sales Practices. Conventional salesman runs after, literally, everybody everywhere. This leads to a wastage of precious resources, like time and money. Using logistic regression, we can narrow down our search by finding those leads who have a higher probability of becoming a customer.
Example: Will the Employee Leave the Company?
Employee retention is a key strategy for HR managers. This is important for the sustainable growth of the company. But in some industries, like Information Technology, employee attrition rate is very high. Using Logistic regression we can build some models which will predict the probability of an employee leaving the organization within a given span of time, say one year. This technique can be applied on the existing employees. Also, it can be applied in the recruitment process. So, we are basically talking about the probability of occurrence or non — occurrence of something.
The Principles Behind Logistic Regression
In simple linear regression, we saw that the outcome variable Y is predicted from the equation of a straight line: Yi = b0 + b1 X1 + εi in which b0 is the intercept and b1 is the slope of the straight line, X1 is the value of the predictor variable and εi is the residual term. In multiple regression, in which there are several predictors, a similar equation is derived in which each predictor has its own coefficient.
In logistic regression, instead of predicting the value of a variable Y from predictor variables, we calculate the probability of Y = Yes given known values of the predictors. The logistic regression equation bears many similarities to the linear regression equation. In its simplest form, when there is only one predictor variable, the logistic regression equation from which the probability of Y is predicted is given by:
P(Y = Yes) = 1/ [1+ exp{ — (b0 + b1 X1 + εi )}]
One of the assumptions of linear regression is that the relationship between variables is linear. When the outcome variable is dichotomous, this assumption is usually violated. The logistic regression equation described above expresses the multiple linear regression equation in logarithmic terms and thus overcomes the problem of violating the assumption of linearity. On the hand, the resulting value from the equation is a probability value that varies between 0 and 1. A value close to 0 means that Y is very unlikely to have occurred, and a value close to 1 means that Y is very likely to have occurred.
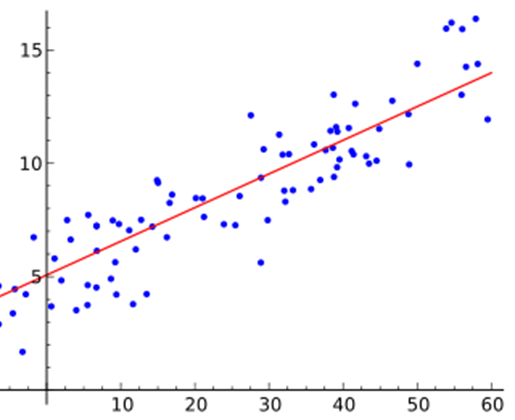
Why Can’t We Use Linear Regression?
One of the assumptions of linear regression is that the relationship between variables is linear. When the outcome variable is dichotomous, this assumption is usually violated. The logistic regression equation described above expresses the multiple linear regression equation in logarithmic terms and thus overcomes the problem of violating the assumption of linearity. On the hand, the resulting value from the equation is a probability value that varies between 0 and 1. A value close to 0 means that Y is very unlikely to have occurred, and a value close to 1 means that Y is very likely to have occurred. Look at the data points in the following charts. The first one is for Linear Regression and the second one for Logistic Regression.
How Do We Get Equation?
In case of linear regression, we used ordinary least square method to generate the model. In Logistic Regression, we use a technique called Maximum Likelihood Estimation to estimates the parameters. This method estimates coefficients in such a way that makes the observed values highly probable, i.e. the probability of getting the observed values becomes very high.
Comparison: Discriminant Analysis and Logistic Regression
Discriminant Analysis deals with the issue of which group an observation is likely to belong to. On the other hand, logistic regression commonly deals with the issue of how likely an observation is to belong to each group, i.e. it estimates the probability of an observation belonging to a particular group.
Discriminant Analysis is more of a classification technique like Cluster analysis.
Comparison: Linear Probability Model and Logistic Regression
The simplest binary choice model is the linear probability model, where as the name implies, the probability of the event occurring is assumed to be a linear function of a set of explanatory variables as follows:
P(Y = Yes) = b0 + b1 X1 + εi
whereas the equation of logistic regression is as follows:
P(Y = Yes) = 1/ [1+ exp{ — (b0 + b1 X1 + εi )}]
You may find a great resemblance of Linear regression with the Linear Probability Mod-el. From expectation theory, it can be shown that, if you have two outcomes like yes or no, and we regress those values on an independent variable X, we get a LPM. In this case, we code yes and no as 1 and 0 respectively.
Why Can’t We Use Linear Probability Model?
The reason is the as why we cannot use the linear regression for a dichotomous out-come variable discussed in the last slide. Moreover, you may find some negative probabilities and some probabilities greater than 1! And the error term will make you crazy. So we have to again study Logistic Regression. NO CHOICE!
Time for Mathematics
If we code yes as 1 and no as 0, the logistic regression equation can be written as follows:
Now if we divide probability of yes by the probability of no, then we get a new measure called ODDS. Odds shouldn‘t be confused with probability. Odds is simply the ratio of probability of success to probability of failure. Like we may say, what‘s the odds of India winning against Pakistan. Then we are basically comparing the probability of India winning to probability of Pakistan winning.
If we take natural logarithm on the both sides, we have:
This is why Logistic regression is also known as Binary Logit Model.
Change In Odds
If we change X by one unit then the change in Odds is given by:
Now if we divide the 2nd relation by the 1st one, we get eβ. So if we change X by 1 unit, then odds changes by a multiple of eβ. So the expression (eβ- 1)* 100% gives the percentage change. Remember this kind of understanding is valid only when X is continuous. When X is categorical, we refer to Odds Ratio.
Odds Ratio
Suppose we are comparing the odds for a Poor Vision Person getting hit by a car to the odds for a Good Vision Person getting hit by a car.
Suppose, the accident is encoded as 1.
Let P(Y =1| Poor Vision) = 0.8
& P(Y =1| Good Vision) = 0.4
So, P(Y = 0| Poor Vision) = 1–0.8 = 0.2
& P(Y =0| Good Vision) = 1–0.4 = 0.6
So, Odds( Poor Vision getting hit by a car) = 0.8 / 0.2 = 4
& Odds( Good Vision getting hit by a car) = 0.4 / 0.6 = 0.67
So, Odds Ratio = 4/ 0.67 = 6
The Odds ratio implies as we move from a good vision person to a poor vision person, the odds of getting hit by a car becomes 6 times.
Developing The Model: Model Convergence
In order to estimate the logistic regression model, the likelihood maximization algorithm must converge. The term infinite parameters refers to the situation when the
likelihood equation does not have a finite solution (or in other words, the maximum likelihood estimate does not exist). The existence of maximum likelihood estimates for the logistic model depends on the configurations of the sample points in the observation space. There are three mutually exclusive and exhaustive categories: complete separation, quasi-complete separation, and overlap.
Assessing the Model
We saw in multiple regression that if we want to assess whether a model fits the data, we can compare the observed and the predicted values of the outcome by using R2 . Likewise, in logistic regression, we can use the observed and predicted values to assess the fit of the model. The measure we use is the log — likelihood.
The log-likelihood is therefore based on summing the probabilities associated with the predicted and actual outcomes. The log — likelihood statistic is analogous to the residual sum of squares in multiple regression in the sense that it is an indicator of how much unexplained information is there after the model has been fitted. It‘s possible to calculate a log-likelihood for different models and to compare these models by looking at the difference between their log-likelihoods. One use of this is to compare the state of a logistic regression against some kind of baseline model. The baseline model that‘s usually used is the model when only the constant is included. If we then add one or more predictors to the model, we can compute the improvement of the model as follows:
Now, what we should do with the rest of the variables which are not in the equation. For that we have a statistic called Residual Chi — Square Statistic. This statistic tells us that the coefficients for the variables not in the model are significantly different from zero, in other words, that the addition of one or more of these variables to the model will significantly affect its predictive power.
Testing of Individual Estimated Parameters
The testing of individual estimated parameters or coefficients for significance is similar to that in multiple regression. In this case, the significance of the estimated coefficients is based on Wald‘s statistic. The statistic is a test of significance of the logistic regression coefficient based on the asymptotic normality property of maximum likelihood estimates and is estimated as:
The Wald statistic is chi-square distributed with 1 degrees of freedom if the variable is metric and the number of categories minus 1 if the variable is non-metric.
The Hosmer-Lemeshow Goodness-of-Fit Test
The Hosmer and Lemeshow goodness of fit (GOF) test is a way to assess whether there is evidence for lack of fit in a logistic regression model. Simply put, the test compares the expected and observed number of events in bins defined by the predicted probability of the outcome. The null hypothesis is that the data are generated by the model developed by the researcher.
Hosmer Lemeshow test statistic:
where Oi is the observed frequency of the i-th bin, Ni is the total frequency of the i-th bin. Пi is the average estimated probability of the i-th bin.
Statistics Related to Log-likelihood
AIC (Akaike Information Criterion) = -2log L + 2(k + s), k is the total number of response level minus 1 and s is the number of explanatory variables.
SC (Schwarz Criterion) = -2log L + (k + s)Σj fj , fj is the frequency of the j th observation.
Cox and Snell (1989, pp. 208–209) propose the following generalization of the coefficient of determination to a more general linear model:
where n is the sample size and L(0) is the intercept only model,
So,
All these statistics have similar interpretation as the R2 in Linear Regression. So, in this part we are trying to assess how much information is reflected through the model.
Understanding the Relation between the Observed and Predicted Outcomes
It is very important to understand the relation between the observed and predicted outcome. The performance of the model can be benchmarked against this relation.
Simple Concepts
Let us consider the following table.
In this table, we are working with unique observations. The model was developed for Y = Yes. So it should show high probability for the observation where the real outcome has been Yes and a low probability for the observation where the real outcome has been No.
Consider the observations 1 and 2. Here the real outcomes are Yes and No respectively, and the probability of the Yes event is greater than the probability of the No event. Such pairs of observations are called Concordant Pairs. This is in contrast to the observations 1 and 4. Here we get the probability of the No is greater than the probability of Yes. But the data was modeled for P(Y = Yes). Such a pair is called a Discordant Pair. Now consider the pair 1 and 3. The probability values are equal here, although we have opposite outcomes. This type of pair is called a Tied Pair. For a good model, we would expect the number of concordant pairs to be fairly high.
Related Measures
Let nc , nd and t be the number of concordant pairs, discordant pairs and unique observations in the dataset of N observations. Then (t — nc — nd ) is the number of tied pairs.
Then we have the following statistics:
In ideal case, all the yes events should have very high probability and the no events with very low probability as shown in the below chart.
But the reality is somehow like the right chart. We have some yes events with very low probability and some no events with very high probability.
What Should be the Cut-point Probability Level?
It is a very subjective issue to decide on the cut-point probability level, i.e. the probability level above which the predicted outcome is an Event i.e., Yes. A Classification Table can help the researcher in deciding the cutoff level.
A Classification table has several key concepts.
Other Measures Related to Classification Table
Receiver Operating Characteristic Curves
Receiver operating characteristic (ROC) curves are useful for assessing the accuracy of predictions. In a ROC curve the Sensitivity is plotted in function of 100-Specificity for different cut-off points of a parameter. Each point on the ROC curve represents a sensitivity/specificity pair corresponding to a particular decision threshold. The area under the ROC curve (AUC) is a measure of how well a parameter can distinguish be-tween two groups. In our case the parameter is the probability of the event.
ROC curve shows sensitivity on the Y axis and 100 mi-nus Specificity on the X axis. If predicting events (not non-events) is our purpose, then on Y axis we have Proportion of Correct Prediction out of Total Occurrence and on the X axis we have proportion of Incorrect Prediction out of Total Non-Occurrence for dif-ferent cut-points.
If the ROC curve turns out to be the red straight line, then it implies that the model is segregating cases randomly.
