Hello Guys in this post we will cover whole mathematical intuition of linear regression. All the material used in post are derived from Prof.Andrew NG lectures.
For this tutorial we will consider salary Dataset which have two columns viz. Experiance and Salary.Depending upon experiance we will predict salary.
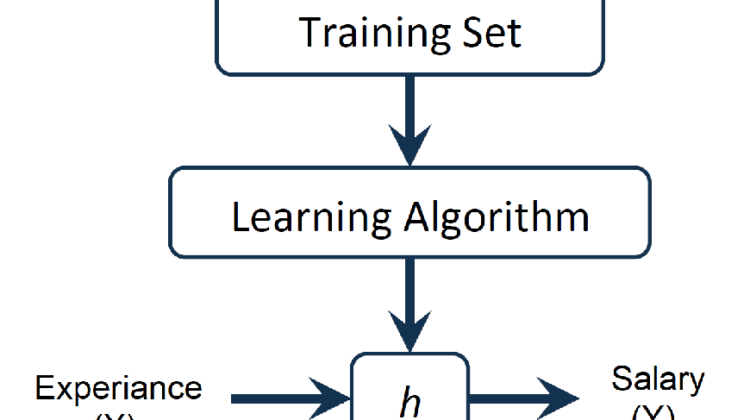
Following Image shows the representation of the model.It has three components viz. Training Set,Learning Algorithm,Hypothesis.
Hypothesis :- Hypothesis is the function which predicts the values using given inputs. More theoretically “It is explanation about relationship between data Popularity that is interpreted Probabilistically”
Now let us represent the Hypothesis:-
Both the equation in above figure are same.(Idealogy of representing them is just to clear the doubt about them since first function is used in Prof.Andrew NG lecture).We will use second function in this tutorial .
Now We have hypothesis/Equation for line. We need to find the best fit line to the given dataset and using that best fit line we will calculate the optimal value for C and m.And those values will be used for further prediction.
For Deriving the values for C and m we need loss Function.
Loss Function :- It Computes the error between Predicted value and actual value for single training example.
Cost Function :- It is Function that measures the performance of machine Learning for whole data set .
In This tutorial we are summing loss function from i=0 to n,so there is no need of cost function.
We will use the Mean Squared Error function to calculate the loss.
Yi = Actual Value in Training Example.
Y̅i = Predicted Value.
n = Number of Training Examples.
and in hypothesis representation we have seen Y̅i= hθ(X) Hence we can modify the loss function as :-
Lets Substitute value of hθ(X), Therefore equation becomes as follow:-
So Now we will find the value of m and c such that they have less mean squared error .for doing this we have algorithm called Gradient Descent.
Gradient Descent is iterative algoritm,which is use to find the minimum of the given function.
Consider above image, We can see that when slope is steep then algorithm takes long step.and when it approaches to the minimum then step size is very small.Here our goal is minimum.
Let’s try applying gradient descent to m and C step by step:
- Initially let m = 0 and C= 0. Let α be learning rate. α controls the how bigger step will be. α could be a small value like 0.0001 for good accuracy.
- Calculate the partial derivative of the loss function with respect to m, and c .Consider above Equation for reference purpose.Lets find Derivative terms:-
3. After we get this terms we will simply update the values of m and c that we have assumed to be 0 in above steps.So update are as :-
We repeat this process until our loss function is a very small or ideally 0 . The value of m and c that we are left with now will be the optimum values.These values can now use to predict the salary of person by given experiance.
In the next post we will implement this with code and dataset.
