By Mehmet Soyer
Machine Learning (makine öğrenmesi) gözetimli öğrenme (supervised lerarning) ve gözetimsiz (unsupervised leraning) öğrenme, pekiştirmeli öğrenme (reinforcement learning) ve diğer olarak olarak dört gruba ayrılır. Gözetimli öğrenme yöntemleri “Regresyon” , “Sınıflama” , “Ağaç Yöntemleri” iken gözetimsiz öğrenme yöntemi ise “Kümeleme” ve “Boyut İndirgeme” olarak ifade edilebilir.
Gözetimli öğrenmede araştırılmak istenen konu hakkındaki girdi (X) ve çıktı (Y) değişkeni bilinirken, bu girdi ve çıktı arasındaki fonksiyon belirlenmeye çalışılır. Böylece farklı girdi (X) değerleriyle karşılaşıldığında gözlemlerin karşılık geldiği (Y) çıktı değişkeni kolayca tahmin edilebilir.
Bu çalışmamda da gözetimli öğrenme yöntemlerinden ‘Linear Regression’ kullanarak bir model oluşturacağım. Yazıma linear regresyonu tanımlayarak başlamak isterim.
Linear (doğrusal) regresyon, değişkenler arasındaki ilişkilerin belirlenmesinde kullanılan bir regresyon yöntemidir. Linear regresyonda bağımlı değişken sayısı bir iken bağımsız değişken sayısı bir ya da birden fazla olabilir. Lineer regresyon analizindeki amaç, gerçek verilere en uygun tahmini değerler üreterek bağımlı değişkeni en iyi açıklayan değişkenler arasındaki ilişkiyi bulmaktır.
Basit gösterimiyle lineer regresyon modeli;
Y = β0 + β1 X1 + βk Xk + ε
şeklinde ifade edilir. Burada,
- Y = bağımlı değişkeni (elde edilmek istenen sonucu), tahmini
- βo = sabit değer (constant), aynı zaman da y eksenini kestiği noktayı
- β1 = kat sayı(coefficient), çizilecek doğrunun eğimini
- βk = k’ nıncı parametreyi
- Xk = k’ nıncı bağımsız değişkeni
- X1 = bağımsız değişkeni
- ε = hata tahmini ifade eder.
Linear regresyon parametrelerini yorumlarken X1’deki bir birimlik değişime karşılık Y, X1’in parametre katsayısı kadar değişim gösterir şeklinde yorum yapılabilir.
Evet lineer regresyona değindikten sonra artık örneğe geçebilirim 🙂
Bu yazımda Python ile makine öğrenmesi algoritmaları kullanarak Kaggle üzerinden elde ettiğim New York, Kalifornia ve Floarida’da bulunan 50 startup firmasının verilerini kullandım. Bu verilerde 50 startup firmasının kar, pazarlama harcaması, yönetici ve çalışan sayısı, Ar-Ge Harcamaları, eyaletler gibi değişkenler mevcuttu. Bağımlı değişken olarak kar, bağımsız değişkenleri ise eyaletler hariç diğer üç değişken olarak ifade ettim. Açıkçası lineer regresyon sonucu 50 startup firmasının karına etki eden değişkenleri belirlemek istedim.
Bunun için Jupyter Notebook üzerinden Python kodu yazmaya başlayabiliriz 🙂
TANIMLAYICI İSTATİSTİKLERİN BELİRLENMESİ
Üstteki tabloda ihtiyacımız olacak Python kütüphanelerini import edip, head() fonksiyonuyla veri setine erişip ilk beş satırı görebiliriz.
Veri setimizin son beş satırını görmek için tail() fonksiyonunu kullanırız. head() ve tail() fonksiyonları default olarak beş alt ya da üst satırı ifade eder. Eğer head(3) ya da tail(3) yazmış olsaydık sırasıyla ilk 3 satır ve son 3 satırı bize gösterecekti.
info() fonksiyonu ise bize veri setimiz hakkında bilgilendirme sunar.
Veri setimizde yer alan verilerin veri tipini değiştirmek istediğimizde astype() fonksiyonunu kullanabiliriz. Üstte “State” değişkeninin object yani string tipinde geldiğini görebiliriz.
shape(satır,sütun) fonksiyonu ise bize veri setimizin satır ve sütun değerlerini verir. Bu veri seti 50 satır ve 5 sütundan oluşmaktadır.
size() fonksiyonu, veri setinde bulunan toplam eleman sayısını ifade eder.
isnull().sum() fonksiyonu değişkenlerde kaç adet bilinmeyen değer olduğunu ifade eder.
describe() fonksiyonuyla verinin standart sapma değerleri, sayısı, ortalaması, maksimum, minimum gibi bilgileri edinilir.
columns() fonksiyonu ile de veri seti içerisindeki sütun isimleri öğrenilir.
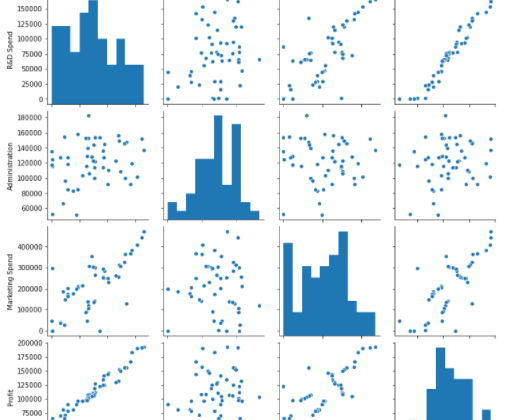
VERİLERİN GÖRSELLEŞTİRİLMESİ
Bir dağılıma hızlıca göz atmanın en kolay yolu distplot() fonksiyonudur. Histogram, nümerik değişkenlerin dağılımlarını görselleştirmede kullanılır. Bağımlı değişkenin (“Profit”) nasıl dağıldığını görebiliriz.
Korelasyon, olasılık kuramı ve istatistikte iki rassal değişken arasındaki doğrusal ilişkinin yönünü ve gücünü belirtir. İki değişken arasındaki korelasyon -1 ve 1 arasındadır. Korelasyon katsayısı 1’e yaklaştıkça pozitif yönde doğrusal ilişki artacak,-1’e yaklaştıkça negatif yönde doğrusallık artacaktır.
Korelasyon analiziyle bağımlı ve bağımsız değişkeneler arasındaki ilişkiyi belirleyebiliriz. Bu değişkenler arasındaki ilişkiye bakıldığında, “Kar” değişkeni ile “Ar-Ge Harcamalarının” ve “Pazarlama Harcamaları” arasında pozitif yönlü yüksek bir ilişki olduğu görülmektedir.
heatmap yine benzer şekilde veriler arasındaki kolerasyonu gösterir ve bu değerleri 0 ile 1 arasında değere ifade eder. Elde edilen değer ne kadar 1’e yakın ise iki veri arasında yüksek korelasyon var demektir. Örnekte, “Kar” ile “Ar-Ge Harcamaları” arasında 0.97’lik, “Pazarlama Harcamaları” arasında ise 0.75’lik pozitif yönlü doğrusal ilişki vardır.
Veri setindeki değişkenlerin bağımlı değişken olarak atanması ve analiz için gerekli olmayan değişkenlerin veri setine dahil edilmemesi için gerekli kodlar yazılır.
En Küçük Kareler (EKK) yöntemiyle oluşturulan modelin özeti yukarıda özetlenmiştir.
Veriyi Eğitim ve Test Olarak Ayırmak
Verilerin yüzde 80’i ile modeli kurarken, yüzde 20’si ile kurduğumuz modelin doğruluğunu ölçüyoruz. Pareto ilkesi ile yapılan bu yüzdelik ayrım veri bilimciler için oldukça önemli. Çünkü tahmin başarımızın yüksek olması için elimizde oldukça fazla veri olmasını isteriz. Fakat test edebilmek için de kenara veri ayırmamız gerekir. İşte burada sonuçların yüzde 80’inin nedenlerin yüzde 20’lik kısımdan geldiğini düşünerek test etmek için yüzde 20’lik kısmı ayırırız ve buradaki sonuçlarımızı raporlarız (Kaynak: Nehir Günce Daşcı).
Veri setinde 50 kayıt var bunun 30’unu eğitim, 10’unu test için ayırdığımızda test_size değeri 0,20 olarak belirlenir.
Kodda random_state’ten bahsetmezsek, kodumuzu her çalıştırdığımızda yeni bir rastgele değer oluşturulur ve train ve test veri kümeleri her seferinde farklı değerler alır. Ancak, random_state (random_state = 42 veya başka bir değer) için her seferinde belirli bir değer kullanırsak, sonuç aynı olacaktır. Yani train ve test veri kümelerinde aynı değerler olacaktır.
Makine Ögrenme işlemi tamamlandıktan sonra artık tahmin bölümüne geçebiliriz. Burada predict fonksiyonu kullanılır. Görselde görüldüğü üzere tahmin değerleri ve veri seti içerisinde karşılaştırma yapabileceğim değerler gösterilmektedir.
Veri seti içerisindeki değerler ile tahmin değerlerimin gösteriminde doğrusal fit edilmiş çizgi görülmektedir.
mean_absolute_error ve mean_squared_error istatiksel olarak performans ölçümleri için kullanılır. mean_absolute_error hatanın mutlak ortalaması olarak nitelendirilir. mean_squared_error ise hatanın kareler ortalaması olarak nitelendirilir. Hata değerinin büyüklükleri ortak ise “mse” kullanılır (Kaynak: Ensar Erdoğan).
