Deep Learning, which is based on the Multilayer Neural Networks has achieved state-of-the-art results in most of the domains as of today. In this post, we will look at the Universal Approximation Theorem — one of the fundamental theorems on which the entire concept of Deep Learning is based upon. We will make use of lego blocks analogy and illustrations to understand the same.
“Neural Networks have an excellent Representation Power of Functions and a Feed Forward Neural Net with one hidden layer with finite number of neurons can represent any continuous function”
In order to make sense of it, let us split the theorem into multiple chunks —
👉 Representation Power of Functions
👉 Feed Forward Neural Net
👉 Hidden layer with a finite number of neurons
�� Represent any continuous function
- A function defines the relationship between a set of inputs and corresponding outputs. Functions can be both continuous or discrete in nature.
- Functions are widely used in Machine Learning concepts such as Loss Functions. In fact, the entire Machine Learning Model can be considered as a function that takes in inputs and provides output.
- Our objective in ML is to minimize the loss functions and we do this by taking the gradient, i.e the first-order derivative of the loss function with respect to the input parameters such as weights and biases.
- Hence differentiability is an important consideration in Machine Learning, we always prefer continuous functions mainly because of their differentiable-at-all-points attribute.
- Since, we compute the gradient, which is a first-order derivative to minimize the loss function, we always prefer continuous functions.
Now let us move one step ahead and understand why do we really need complex functions and why we need something like Neural Network to approximate the same.
- We have several types of relationships in real life namely linear functions, quadratic functions, non-linear functions, etc.
- Linear function: Function that models a linear relationship for e.g the amount of fuel used has a linear relationship with the distance traveled.
- Quadratic function: Function that models quadratic relationship for e.g the path traced by a golf ball during the shot exhibits quadratic relationship.
- Non-linear function: Let us look at few examples of non-linear relationships. For e.g, a drug medication provided to a patient may not display desirable outcomes until a threshold level; triangulation of signals from the GPS satellites are non-linear in nature.
- Hence, in order to model such complex relationships, a simple linear or quadratic function may not be the most appropriate one.
- Therefore, we must require Complex functions to model complex non-linear relationships.
This is where the need to approximate any complex functions and model non-linearity comes into the picture. Now, let us look at how Neural Networks can help on the same.
In a traditional programming scenario, where the input and the guiding rules are programmed, resulting in output.
In Machine Learning, we feed the input and desired output into the Machine Learning Model, which then ‘learns’ the function and provides the set of rules (also known as function or model).
The Computation segment in the above flow diagram is implemented by a Machine Learning model or a Deep Neural Network. The Neural Networks, as the name states is a network of neurons, stacked in multiple layers namely the input layer which takes the input, the hidden layer which does the feature engineering, and the output layer which provides the target value.
Every unit of neuron has the following attributes —
⚡️ an input
⚡️ a weight associated with it
⚡️ a bias unit associated with it
⚡️ and an activation function that decides whether the neuron will fire or not
⚡ ️output
During a Neural Network training phase, the weights and bias values will be applied to the input, and then based on the activation function used, the final output would be provided by the neuron.
For e.g, let us consider the below representation — here x1, x2…xn are the inputs with w1, w2…wn their corresponding weights; b is the bias unit and ‘f’ is the activation function. The final output of this neural unit would be given by the function f(ΣXi Wi + b).
If ‘f’ is a sigmoid function, then the output would range from 0 to 1; similarly, for a tanh function, the output would range from -1 to 1. Now that we have understood the basic structure of a Neural Network, let us move ahead and understand how this structure helps to model complex relationships using a concept called ‘Representation Power of Functions’.
- According to the Universal Approximation Theorem, a network of neurons can approximate and model any complex continuous function.
- This is carried out by tuning the values of weights and bias parameters associated with each of the neuron units along with its linear/non-linear activation functions.
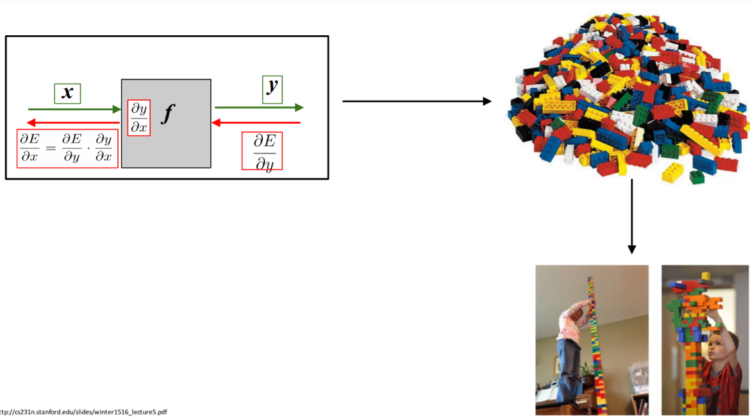
Let us take an analogy of building blocks used by my three-year-old to understand it better. Kids are the best architects when it comes to creating different looking structures from the same set of blocks.
Using the same set of blocks, numbers and vehicles and animals can be formed (architectured). This is analogous to the function approximation done by Neural Networks.
Weights and biases in the input, hidden and output layer along with activation functions act as the basic building blocks of a Neural Network. By tweaking and using different combinations of such building blocks, we are able to approximate any complex function.
Let us take a curvilinear function shown in the below output layer — this function can be approximated using two linear neurons (wx+b) with a linear activation function.
In a Neural Network layer,
Positive weights → express the input in a positive relation
Negative weights → express the input in a negative relation
Zero weights → suppress the input
Activation function → introduces non-linearity in output
Hence, the weights play a major role in performing ‘Feature Engineering’, creating millions of parameters from the original inputs and then weighting and de-weighting the parameters by minimizing the overall network loss.
The hierarchical nature of Neural Networks is best suited to learn the hierarchy of knowledge to solve real-world problems.
Let us see a few more illustrations to understand the same with visual clarity.
In order to achieve the final output function that looks like a tower, we can combine both the graphs (outputs from a sigmoid activation function), and then tweak the weights at the hidden layer. Let us take the weights +1 and -1 in the hidden layer and we can see that the Neural Network has rightly predicted the output function.
The most interesting thing in this learning process is that we need not change the weights manually to get the desired output, rather the weight and bias values would be auto-calculated and updated based on a loss optimization algorithm called ‘Gradient Descent’ during Backpropagation.
👉 Universal Approximation Theorem: Neural Networks have an excellent Representation Power of Functions and a Feed-Forward Neural Net with one hidden layer with a finite number of neurons can represent any continuous function.
👉 The hierarchical nature of Neural Networks is best suited to learn the hierarchy of knowledge to solve real-world problems.
👉Positive weights → express the input in a positive relation; Negative weights → express the input in a negative relation; Zero weights → suppress the input; Activation function → introduces non-linearity in output
👉 Neurons in Neural Networks are analogous to the lego blocks — the same set of lego blocks can be used to build different structures by slightly tweaking the design every time.
- http://neuralnetworksanddeeplearning.com/
- https://www.youtube.com/watch?v=aPfkYu_qiF4&list=PLyqSpQzTE6M9gCgajvQbc68Hk_JKGBAYT&ab_channel=NPTEL-NOCIITM
- https://www.youtube.com/watch?v=BR9h47Jtqyw&ab_channel=LuisSerrano
- CS231N Convolutional Neural Networks by Andrej Karpathy — Stanford University
- Introduction to Deep Learning course on Udacity
