What Makes College Worth It?

Like most Asian immigrants, my parents emphasized the importance of school, with college graduation as the gateway to the American dream. Because of that, I never questioned whether I should go to college or not. It was more a matter of which one.

Back when I was deciding, I did not do a cost-benefit analysis as I’d done with the model I’ll talk about later, though maybe I should have. Instead, I thought more about two things:

1. Which college felt like Hogwarts, and more importantly,
2. Which college might impress my “chismosa” titas (chismosa is “gossipy” in Tagalog).

Without too much thought, I followed my childhood best friend over to UC San Diego for undergrad, then Columbia University for graduate school. When I finished, I ignorantly thought college would pay in itself. But when I got my first student loan bill and a job offer salary that did not match, my jaw dropped! Who was I to think I could shop for colleges as if I were Cher Horowitz with her daddy’s Credit card?

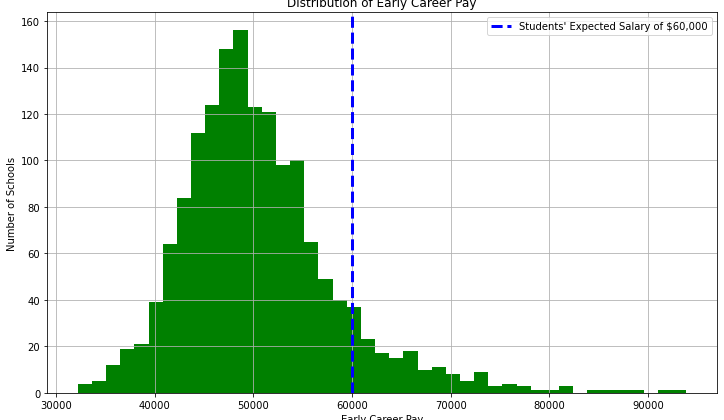
Turns out, I’m not alone. According to a survey conducted by LendEDU, college students expected a median salary of $60,000 after graduating. 52% of college students took out student loans to attend college, and of that number, 17% had trouble paying for it.

This made me question: what makes college worth attending?

Methodology

I looked at over 900 schools (after data cleaning) and 8 school features, listed below (sourced through PayScale, Data.World, and US News & Reports).

1. Meaning Percentage (continuous) — how many graduates find their work meaningful?
2. STEM Percentage (continuous) — what percentage of degrees conferred were STEM-related (Science, Technology, Engineering, Mathematics)
3. School Type (categorical) — engineering, private, religious, art, for sports fans, party school, liberal arts, state, research university, business, sober, ivy league
4. State (categorical) — where the school is located
5. Tuition (continuous) — includes in-state, out-of-state, and room-and-board costs
6. Total Enrollment (continuous) — how many students enrolled in the school
7. Diversity Enrollment (continuous) — enrollment for minority groups (Asian, Black, Hispanic, Native Hawaiian/ Pacific Islander, Native American/ Alaskan Native, women, and non-residents)
8. School Rank (categorical) — I binned rank by Top 50, Top 100, Top 150, Top 200, Top 250, and Over 250 to include the schools not listed in the Top 250.

You can find a preview of the final DataFrame below.

My baseline model used 75% of the data to build a logistic regression model that predicts whether schools have an expected income of $60,000 or more, then used the remaining 25% to test my model’s accuracy. My final model signified which features carry the most weight in predicting salary.

Our null hypothesis claims that the features do not have any impact on expected income. Our alternate hypothesis claims that features do have an impact on expected income.

Our data showcases that early-career salary for college graduates average out to $50,000 and has a median of $49,000. Of all the colleges we looked at, only 10.2% actually have an early-career salary of $60,000 or more.

Because I built a logistic regression model instead of a linear regression model, I engineered the target variable, over_60000, from the early-career salary column, with early-career salaries of $60,000 labeled as True, and early-career salaries of less than $60,000 as False.

Building My Model

# import necessary libraries
import statsmodels as sm 
import sklearn.preprocessing as preprocessing 
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split 
from scipy import stats#Define dependent and independent variables
X = colleges_df.drop(columns=['over_60000'], axis=1)
X = pd.get_dummies(X, drop_first=True, dtype=float)y = colleges_df['over_60000'].astype(float)#Split data into training and testing 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)# Fit model 
logreg = LogisticRegression(fit_intercept=False, C=1e12, solver='liblinear')
model_log = logreg.fit(X_train, y_train)

I used Scikit-learn to build my baseline model by defining my target variable, over_60000, as y, and all the rest of the columns in the DataFrame, my features, as X. I used the get_dummies method to deal with my categorical variables.

Once I fit my data into the model, I checked the results.

Measuring My Model

Because I predicted whether schools will earn graduates an early-income salary of $60,000 or more, I wanted to prioritize my precision score over recall. Remember, precision is calculated from all the predicted values, whereas recall is calculated from all the true values (this blog does a great job explaining the difference). I wouldn’t want to tell a student that the school they’re attending has an expected early-income of $60,000 or more when in reality, it doesn’t. However, it wouldn’t hurt if my model told a graduate their school does not expect an early-career salary of $60,000 or more, but they actually do. A pleasant surprise and delight, I’d say.

The confusion matrix on the left showcases how well my baseline model predicted the test data. My baseline predicted 12 schools had an expected salary of over $60,000, but only 6 schools actually met the criteria, resulting in a 50% precision score. No bueno!

Iterating My Model

Clearly, I still had a lot of work to do to improve my precision score. You can find the iterative process on my GitHub, but to not bore you with the details, here’s a quick summary of it all:

• I toyed with the training size of my data with Scikit-Learn’s train_test_split to see which training size gave the best results
• I trimmed down features based on their statistical significance shown on Statsmodel
• I dealt with class imbalance using SMOTE and by specifying the class weight when fitting my model (though both actually did not do anything to improve my precision score- it actually dropped down to 10%. Like how does a logistic regression model that just predicts True of False score that poorly?)

After multiple iterations, my final model predicted 24 schools met the expected salary target. Of the 24 schools, 18 hold true, resulting in a precision score of 75%, an increase of 25% from my baseline model. Side note: my accuracy score went from 91% to 94% as well. Hallelujah!

My finalized model used 70% of the data to train, left the class imbalance as is, and essentially only used 3 features: rank (Top 50 and Top 100), school type (engineering, for sports fans, liberal arts, and research), and enrollment of minority groups (primarily for Asian graduates and women). The results can be found below.