Simple linear regression is fittingly simple. It is the first algorithm one comes across while venturing into the machine learning territory. However, its genesis lies in statistics. Practitioners later smuggled its applications to machine learning and several other spheres like business and economics as well. Anyone who has taken a first-year undergraduate course in probability and statistics can do simple linear regression. All it entails is finding the equation of the best fit line through a bunch of data points. To do so, you follow a standard protocol, calculate the differences between the actual target values and the predicted values, square them, and then minimize the sum of those squared differences. On the surface, there’s no transparent link between regression and probability. It’s more to do with calculus. But, there’s a far more stirring side to regression analysis concealed by the gratification and ease of importing python libraries.
Zooming in on Regression
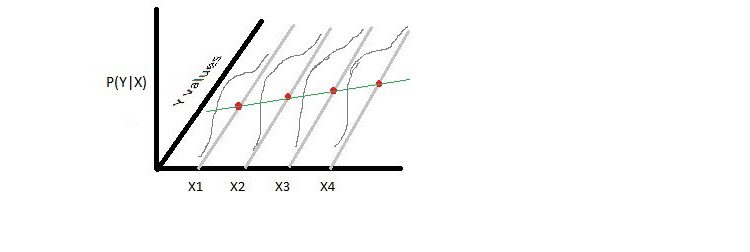
Let’s ponder a simple regression problem on an imaginary dataset where X and Y hold their customary identities-explanatory and target variables. The holy grail with regression, in a nutshell, is to disinter a line adept at approximating target variables(y values) with minimal error. But, hold back. Instead of hounding for the line, think of all x values plotted on the x-axis. Consider parallel lines to the y axis passing through each x. Draw it on paper if it helps, something like shown below.
What do the grey lines represent? Well, if you account for turbulent factors present in the real world, then Y could be any value for a given X. For instance, despite studying for the same number of hours, you may score differently on two separate monthly tests. All lines thus designate the range of Y, all real numbers, for each X.
If I now challenge you to estimate the target variable for a given x, how would you proceed? The answer will unveil the probabilistic panorama of regression. Would it not help if I provided you with a conditional probability distribution of Y given X-P(Y|X)? Of course, it would, but there are no means to extract an accurate distribution function. So, we make an assumption, the first of many. Assume the probability of Y given X, P(Y|X), follows a normal distribution. Why normal? Depending on the prior knowledge of the dataset you’re working on, you are free to choose any appropriate distribution. However, for reasons that’ll soon be clear, we’ll resort to normal distribution.
We will represent this probability distribution on the z-axis of the above-drawn plot. As you can see in the image below, P(Y|X) follows a normal distribution. The red dots are the mean of each P(Y|X). Pardon the quality of images. I made them in MS paint for representation purposes.
Unravelling the parameters of the normal distribution
Fine, we established the type of distribution. What about its parameters-mean and variance? To make sound estimates, we need the means and variances of Y for each given X in the dataset. At this point, it’s wise to begin dallying with the regression line, a+bX.
As mentioned before, we hope to find coefficients a and b such that computing a+bx yields the best estimate for real y values. Considering y to be normally distributed, what could be the best estimate? Note that upon randomly drawing values from a normal distribution, one will get the mean value most times. So, it’s wise to bet that a+bX is the mean or expected value of Y|X.
Here lies a conspicuous yet understated fact. Because we assume a+bx to be the expected value of Y|X, we also conjecture that all means lie on the regression line a+bx. This is an obligatory condition to employ regression models. Think of it this way, if the real means didn’t lie on a line, is it sensible to use linear regression? Now you’d be wondering how anyone ascertains the linearity? We can’t because the real values are a mystery. Then, why am I bothering you with it? In practical machine learning, one takes the existence of linearity as granted and proceeds with modelling. Post-modelling tests are anyways available to determine a linear regression model’s accuracy. What’s important here is to be privy to the underlying assumption.
Okay, how to deal with the variance? To maintain homoscedasticity, we assume the variance value to be constant for all Y|X. Homoscedasticity means homogeneity of variance. The concept deserves a separate post of its own. For us, however, it’s sufficient to know that the least-square estimate will be erroneous in its absence. Read till the end, and you shall discover why.
Bayesian panorama of Regression
Understanding things beyond this point requires the knowledge of the Bayes theorem. My undergrad prof used to say, “Class, you would fail to do any appreciable machine learning without knowing Bayes theorem.” So, I’ll skip its detailed explanation in the hope that, as ML enthusiasts, you are chummy with Bayes and his ideas.
Let’s recapitulate what we’ve done so far. We started with an imaginary dataset consisting of explanatory and target variables-X and Y. Then, we attempted to figure out the probability of Y given X. To do so, we assumed Y|X followed a normal distribution with mean a+bX. Ergo, we also established that means of all Y|X lies on the regression line.
Great, it’s time to set on hunt for the holy grail. We need to find the best estimates for a and b. What dictates these estimates? You guessed it right-the data at hand. Parameters a and b should be such that the probability, P(a=A,b=B|data) is maximum.
How to do that? Here comes Bayes to our rescue. According to Bayes theorem:
Hence, we can write
For the rest of the article, I’ll refer to the above equation as Bayes.
Note, without access to reliable data, a and b are indeterminate. They can take any values from the set of real numbers. P(a=A,b=B) is the probability of getting a=A and b=B irrespective of the data values at hand. Say we want to model the regression of ice cream sales with the daily maximum temperature.
Your friend Thomas Bayes, who also happens to be a dessert industry expert, graciously agrees to provide any help with the research. Based on his experience, he models a probability distribution of (A, B). Sweet, you now have a better idea about the most likely values of (A, B). In many situations, though, you will not have the support of a Thomas. Under such helpless conditions, it is supposed that any set of (A, B )is equally likely. Probabilistically speaking, P(A=a1, B=b1), also known as prior probability or just prior, is assumed to be uniformly distributed.
To summarize, priors are uninfluenced by the data, and as the name suggests, they reflect our preliminary notion of a regression model.
Coming back to our problem. We too assume the prior to be uniformly distributed. Our goal was to maximize the right-hand side of Bayes. As P(a=A, b=B) is constant across all sets of (A, B), we can ignore the term.
Next, recognize that P(data) is merely a constant. Why? It’s the total probability of getting the data, a particular set of x,y, across all pairs of a,b. P(data| a=A, b=B) is a real value ranging between 0 and 1 (You’ll soon see why) for each pair of a,b. Thereby, the sum of those probabilities, P(data), is a constant.
Constants on either side of proportionality can be dropped.
P(data|a=A, b=B) is the probability of getting the data, all the provided sets of values (X, Y) given the parameters A and B. It can also be written as P(X,Y|a=A, b=B). According to rules of conditional probability, which I won’t delve deep into, P(X, Y|a=A, b=B) can be further simplified as P(Y|X, a=A, b=B).
Our problem breaks down to maximizing P(Y|X, a=A, b=B). As assumed, P(Y|X) follows a normal distribution with a mean value of a+bX and variance σ². In the provided data, Y could differ from a+bX. Consequently, with P(Y|X, a=A, b=B), we aim to find the probability of getting Y=y from a normal distribution with mean a+bX and variance σ².
Since all Y|X are independent, we can simplify P(Y|X, a=A, b=B) as the product of all individual P(Y=y|X=x, a=A, b=B).
Unearthing the least square approximation function
The probability density function, pdf, for a normal distribution is:
Unlike discrete distributions, continuous distributions don’t define the probability for a distinct point. You can only integrate the pdf over a range of values, say x1<X<x2, and find how likely X is to lie within that boundary.
In our case then we can approximate the following probability by integrating the pdf over a considerably small range.
Carrying with the calculations, we can further write
I apologize to math experts for pulling a dirty trick. To make things easy, I eliminated integration operation and introduced proportionality sign instead of equality. It was all done under the assumption that the integrand dy is the same for all x,y.
Just a few more mathematical manipulations to go. To maximize the daunting looking L, let’s first take a log on both sides.
The first term on the right is a constant. Ergo, algebra necessitates that to maximize log(L), we need to minimize the second term. Now, snoop around the second term. Did you spot something dear? Bingo! You have unearthed the celebrated least square approximation term.
Maximizing L entails minimizing the second term, which happens to be the least square approximation function.
Appreciate the fact that least square approximation is the appropriate procedure for carrying regression analysis under the conditions that:
- Target variable, y, follows a normal distribution for a given x
- All values of the regression parameters are equally likely. That is, the prior follows a uniform distribution
- Variance value is assumed constant for all Y|X. Otherwise, we could not have pulled it out from the summation term
Any deviation from these conditions would result in having to follow an alternate procedure. You’ll have to repeat the entire exercise in such a case.
My aim with the article was to share why we resort to minimizing the sum of squared differences when doing regression analysis. I was staggered the first time I came across this revelation. In pursuit of doing cool stuff in machine learning, many often gloss over the underlying mathematics. Perhaps, one may never professionally require that knowledge. But by turning a blind eye to it, you miss out on the beauty governing machine learning. It’s an eyeful.
